Chương VII: Công thức thấu kính, chứng minh công thức thấu kính
Chương VII: Cấu tạo quang học của mắt, các tật của mắt và cách khắc phục
1/ Chứng minh công thức thấu kính hội tụ
xét trường hợp vật sáng AB đặt vuông góc với trục chính của thấu kính hội tụ.
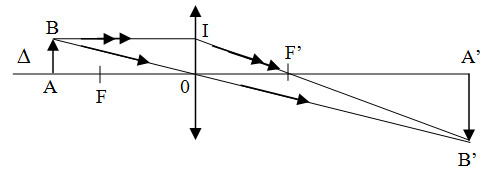
a/ trường hợp vật thật qua thấu kính hội tụ cho ảnh thật
Chương VII: Công thức thấu kính, chứng minh công thức thấu kính
ΔA’B’O đồng dạng với ΔABO =>
A′B′AB=A′OAO=d′dA′B′AB=A′OAO=d′d (1)
ΔA’B’F’ đồng dạng với ΔOIF’ =>
A′B′OI=A′F′OF′A′B′OI=A′F′OF′=OA′−OF′OF′=d′−ffOA′−OF′OF′=d′−ff (2)
từ (1) và (2) => d′d=d′−ffd′d=d′−ff => 1f=1d+1d′1f=1d+1d′
b/ trường hợp vật thật qua thấu kính hội tụ cho ảnh ảo
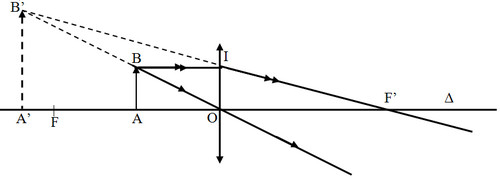
ΔABO đồng dạng với ΔA’B’O =>
A′B′AB=A′OAO=d′dA′B′AB=A′OAO=d′d (1)
ΔOIF’ đồng dạng với ΔA’B’F’ =>
A′B′OI=A′B′AB=A′F′OF′A′B′OI=A′B′AB=A′F′OF′=OA′+OF′OF′=d′+ffOA′+OF′OF′=d′+ff (2)
từ (1) và (2) => d′d=d′+ffd′d=d′+ff => 1f=1d−1d′1f=1d−1d′
2/ Chứng minh công thức thấu kính phân kỳ
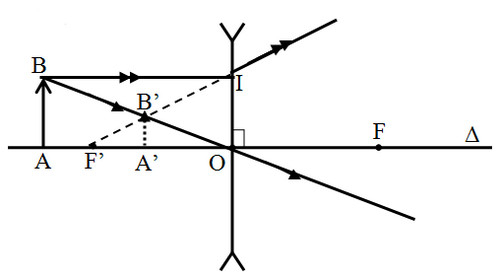
ΔABO đồng dạng với ΔA’B’O =>
A′B′AB=A′OAO=d′dA′B′AB=A′OAO=d′d (1)
ΔOIF’ đồng dạng với ΔA’B’F’ và (OI = AB) =>
A′B′AB=A′F′OF′A′B′AB=A′F′OF′=OF′−OA′OF′=f−d′fOF′−OA′OF′=f−d′f (2)
từ (1) và (2) => d′d=f−d′fd′d=f−d′f => 1f=1d′−1d1f=1d′−1d
3/ Công thức thấu kính dùng chung và qui ước dấu
