Phương pháp giải bài tập các định luật Newton đầy đủ
Dấu của các đại lượng vật lý, chiều dương, hệ qui chiếu.
Phương pháp giải bài tập các định luật Newton đầy đủ, phép chiếu các đại lượng véc tơ lên các trục tọa độ cho trước.

Phương pháp giải bài tập các định luật Newton đầy đủ
I/ Phương pháp tính độ lớn véc tơ lực, cách chọn và chiếu véc tơ lực
1/ Tính độ lớn của các véc tơ lực sử dụng kiến thức toán véc tơ cho vật lý
xem tại đây: Toán véc tơ cho vật lý
2/ Tính độ lớn của các véc tơ lực sử dụng phương pháp chiếu véc tơ lên các phương cho trước.
Tổng quát về cách chiếu véc tơ lên các trục cho trước như hình minh họa.
III/ Vận dụng giải các bài tập định luật Newton:
1/ Các bước giải bài tập định luật Newton truyền thống
- bước 1: phân tích các lực tác dụng vào vật hoặc hệ vật
xem thêm: Các lực cơ bản, phân tích lực, biểu diễn lực, vẽ lực
- bước 2: chọn hệ qui chiếu gắn với vật
- bước 3: chiếu véc tơ lực lên các phương trong hệ qui chiếu thiết lập hệ phương trình liên quan giữa các lực từ đó tính ra giá trị cần tính.
2/ Các ví dụ cụ thể (từ dễ đến khó)
Bài tập 1: Vật m trượt trên mặt phẳng ngang có hệ số ma sát µ dưới tác dụng của lực F theo phương ngang. Lấy g=10m/s2.
a/ Tính gia tốc của vật
b/ Nếu vật trượt đều xác định hệ số ma sát trượt
c/ sau khoảng thời gian t lực F thôi tác dụng, tính quãng đường vật đi thêm được trước khi dừng lại.
các lực tác dụng vào vật như hình vẽ,
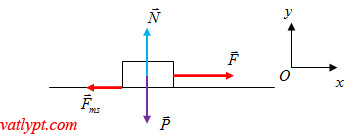
Định luật II Newton:
⃗PP→ + ⃗NN→ + ⃗FF→ + →FmsFms→ = m⃗aa→
Chiếu lên trục Ox: -Fms + F = ma (1)
Chiếu lên trục Oy: N – P = 0 => N = P
=> Fms = µN = µP = µ.mg (2)
thay (2) vào (1) => -µ.mg + F = ma => a
b/ vật trượt đều => a = 0 =>
⃗PP→ + ⃗NN→ + ⃗FF→ + →FmsFms→ = 0
Chiếu lên Ox : -Fms + F = 0 => Fms = F
Chiếu lên Oy: N – P = 0 => N = P
Fms = µN = µP = µ.mg = F => µ = F/mg
c/ F = 0
⃗PP→ + ⃗NN→ + →FmsFms→ = m→a′a′→
Chiếu lên Ox: -Fms = ma’ => a’ = -Fms/m
Chiếu lên Oy: N – P = 0 => N = P
Fms = µN = µP = µ.mg => a’ = -µg
Rút gọn:
Vật chuyển động dưới tác dụng của lực theo phương ngang, chọn chiều dương là chiều chuyển động của vật => phương trình định luật II Newton
F – Fms = ma => F – µ.mg = ma đây chính là phương trình bạn sẽ sử dụng để giải các bài tập liên quan tương tự, bạn muốn .
Quan trọng:
Fms = µN với N có bản chất là áp lực (lực nén của vật lên bề mặt tiếp xúc: điểm đặt tại mặt tiếp xúc phương vuông góc với mặt tiếp xúc, chiều ngược chiều với phản lực)
vậy tại sao các hình vẽ đều sử dụng phản lực mà không phải là áp lực?
– khi áp dụng định luật II Newton ta chỉ xét các lực tác dụng vào vật m
– áp lực có điểm đặt tại bề mặt tiếp xúc không phải đặt vào vật m
=> ta phải xét phản lực do mặt tiếp xúc gây ra cho vật có điểm đặt tại vật m cùng phương ngược chiều có cùng độ lớn với áp lực.
xem thêm: Lý thuyết – Lực ma sát trượt, lực ma sát nghỉ, lực ma sát lăn
Một số bài toán vật lý trong diễn đàn vật lý phổ thông sử dụng phản lực Q khi biểu diễn về cơ bản N, Q, chỉ là kí hiệu còn bản chất của nó là lực nào bạn phải nắm rõ.
Bài tập 2: Vật m trượt trên mặt phẳng ngang có hệ số ma sát µ dưới tác dụng của lực F hợp với phương ngang góc α. Lấy g=10m/s2. Thiết lập phương trình định luật II Newton dưới dạng độ lớn.
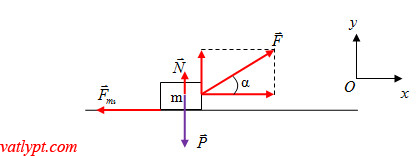
phương trình định luật II Newton
⃗PP→ + ⃗NN→ + ⃗FF→ + →FmsFms→ = m⃗aa→
Chiếu lên Oy: N + Fsinα – P = 0 => N = P – Fsinα = mg – Fsinα
Chiếu lên Ox: Fcosα – Fms = ma
Fms = µN => Fms = µ(mg – Fsinα)
=> Fcosα – µ(mg – Fsinα) = ma => F(cosα + µsinα) – µmg = ma
Bài tập 3: Vật m trượt trên mặt phẳng nghiêng góc α so với phương ngang có hệ số ma sát µ dưới tác dụng của lực F song song với mặt phẳng nghiêng. Lấy g=10m/s2. Thiết lập phương trình định luật II Newton dưới dạng độ lớn trong 2 trường hợp sau:
a/ vật trượt xuống
b/ vật trượt lên
trục Oy vuông góc với mặt phẳng nghiêng, trục Ox song song với mặt phẳng nghiêng
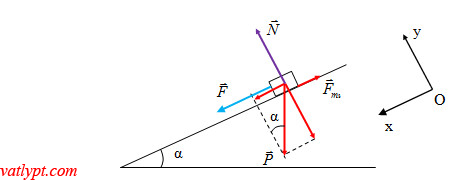
Phương trình định luật II Newton:
⃗PP→ + ⃗NN→ + ⃗FF→ + →FmsFms→ = m⃗aa→
Chiếu lên Oy => N – Pcosα = 0 => N = Pcosα = mgcosα
Fms = µN = µ.mgcosα
Chiếu lên Ox: F + Psinα – Fms = ma => F + mgsinα – µ.mgcosα = ma
b/ Chọn hệ qui chiếu và phân tích các lực như hình vẽ
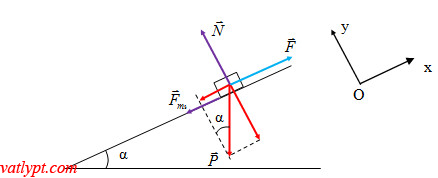
Phương trình định luật II Newton:
⃗PP→ + ⃗NN→ + ⃗FF→ + →FmsFms→ = m⃗aa→
Chiếu lên Oy => N – Pcosα = 0 => N = Pcosα = mgcosα
Fms = µN = µ.mgcosα
Chiếu lên Ox: F – Psinα – Fms = ma => F – mgsinα – µ.mgcosα = ma
Bài tập 3: Vật m trượt trên lên mặt phẳng nghiêng góc α so với phương ngang có hệ số ma sát µ dưới tác dụng của lực F hợp với mặt phẳng nghiêng góc β. Lấy g=10m/s2. Thiết lập phương trình định luật II Newton.
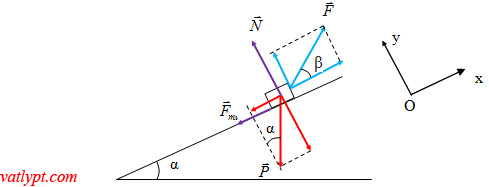
Phương trình định luật II Newton:
⃗PP→ + ⃗NN→ + ⃗FF→ + →FmsFms→ = m⃗aa→
Phương trình định luật II Newton:
⃗PP→ + ⃗NN→ + ⃗FF→ + →FmsFms→ = m⃗aa→
Chiếu lên Oy => N – Pcosα + Fsinβ = 0 => N = Pcosα – Fsinβ = mgcosα – Fsinβ
Fms = µN = µ(mgcosα – Fsinβ)
Chiếu lên Ox: Fcosβ – Psinα – Fms = ma
=> Fcosβ – mgsinα – µ.(mgcosα – Fsinβ) = ma
Bài tập 4: (hệ vật) Cho hệ vật như hình vẽ, thiết lập hệ số ma sát giữa các vật m1; m2 với mặt phẳng ngang là µ. Thiết lập phương trình định luật II Newton cho hệ vật dưới dạng độ lớn.
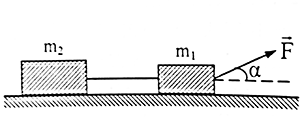
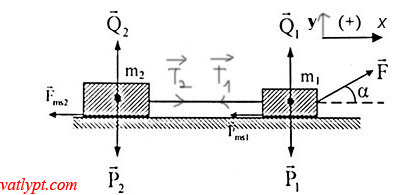
Đối với hệ vật ta phải xét định luật II Newton cho từng vật
Lưu ý: dây căng không giãn => T1 = T2 = T; a1 = a2 = a
vật m1: →P1P1→ + →Q1Q1→ + ⃗FF→ + →Fms1Fms1→ + ⃗TT→ = m1⃗aa→
Chiếu lên Oy: Q1 – P1 + Fsinα = 0 => Q1 = m1g + F.sinα
=> Fms1 = µQ1 = µ(m1g + Fsinα)
Chiếu lên Ox: Fcosα – Fms1 – T = m1a
=> Fcosα – µ(m1g + Fsinα) – T = m1a (2)
Vật (2): →P2P2→ + →Q2Q2→ + ⃗TT→ + →Fms2Fms2→ = m2⃗aa→
Chiếu lên Oy: Q2 – P2 = 0 => Q2 = m2g
=> Fms2 = µQ2 = µm2g
Chiếu lên Ox: T – Fms2 = m2a => T – µm2g = m2a (2)
(1) + (2) => Fcosα – µ(m1g + m2g + Fsinα) = (m1 + m2)a
Bài tập 5: vật m chuyển động với vận tốc v theo phương hợp với phương ngang góc α đến đập vào tường rồi bật trở lại theo định luật phản xạ gương với độ lớn vận tốc không đổi. Tính lực tác dụng vào tường biết thời gian vật va chạm với tường là t.

⃗FF→ = m⃗ama→ = m→v2−→v1tv2→−v1→t
Chiếu lên hệ qui chiếu đã chọn như hình vẽ lưu ý: v2 = v1 = v
F = m[v2cosα – (-v1cosα)]/t = 2m(vcosα)/t
