Chương IV: Bài tập va chạm, đạn nổ
Chương IV: Bài tập thế năng trọng trường, thế năng đàn hồi
Bài tập va chạm, đạn nổ, bảo toàn động lượng, bảo toàn động năng, bảo toàn năng lượng
I/ Tóm tắt lý thuyết
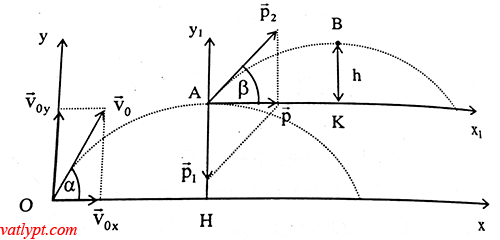
Bài tập 1. Lựu đạn ném từ mặt đất với vận tốc vo = 20m/s theo phương lệch với phương ngang góc α = 30o. Lên tới điểm cao nhất nó nổ thành hai mảnh bằng nhau. Mảnh I rơi thẳng đứng với vận tốc đầu v1 = 20m/s.a/ Tìm hướng và độ lớn của mảnh II.b/ Mảnh II lên tới độ cao cực đại cách mặt đất bao nhiêu.
Chương IV: Bài tập va chạm, đạn nổ
Chọn hệ tọa độ như hình vẽ
Tại điểm cao nhất A vận tốc của v theo phương ngang
vox = vocosα = 10√3 (m/s)
Vị trí A có độ cao là: hA = vo2sin2α/(2g) = 5m
xem thêm: bài tập chuyển động ném xiên
Xét lựu đạn nổ tại A
Định luật bảo toàn động lượng ⃗pp→ = →p1p1→ + →p2p2→
p = 2mv = 20√3; p1 = mv1 = 20m
p22 = p2 + p12 => p2 = 40m => v2 = p2/m = 40 m/s
tan β = p1/p = 1/√3 => β = 30o
b/ độ cao cực đại của mảnh 2 so với A: hB = v22sin2 β/(2g) = 20m
=> độ cao cực đại của mảnh II so với đất: h = hA + hB = 40m
Bài tập 2: Một viên đạn 2kg chuyển động theo phương ngang với vận tốc 250m/s nổ thành hai mảnh. Mảnh khối lượng 1,5kg có vận tốc bằng 250m/s bay thẳng đứng xuống dưới. Hỏi mảnh thứ hai bay theo phương nào? Với vận tốc bằng bao nhiêu?
m=2kg; m1=1,5kg; v=250m/s; v1=250m/s; m2=m – m1=0,5kg
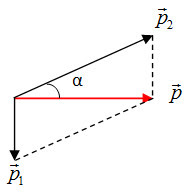
⃗p=→p1+→p2p→=p1→+p2→
Giải
p2=√p2+p21p2=p2+p12=625kg.m/s
=> v2=p2m2v2=p2m2= 1250 (m/s)
tanα=p1pp1p=> α=36,860
Bài tập 3. Một quả lựu đạn bay theo quỹ đạo parobol, tại điểm cao nhất h = 5m, đạn nổ làm hai mảnh khối lượng bằng nhau. Một giây sau khi nổ, một mảnh rơi xuống đất ở ngay phía dưới vị trí nổ, cách chỗ bắn s1 = 17,3m.Hỏi mảnh thứ hai rơi đến đất cách chỗ ném khoảng s2 là bao nhiêu? Bỏ qua sức cản của không khí.

Bài tập 4: Một viên đạn có khối lượng 3kg chuyển động với vận tốc 250√2 m/s thẳng đứng hướng lên nổ thành hai mảnh. Mảnh 2kg có vận tốc 375m/s hợp với phương thẳng đứng góc bằng 450. Tìm vận tốc và hướng bay của mảnh còn lại

m=3kg; v=250√2 m/s; m1=2kg; v1=375m/s; m2=m – m1=1kg. α=45o.
Giải
p2=√p2+p21−2p.p1cos45op2=p2+p12−2p.p1cos45o=750kg.m/s
=> v2=p2m2v2=p2m2= 750 (m/s)
p1=√p2+p22−2p.p2cosα2p1=p2+p22−2p.p2cosα2 => α2=300
Bài tập 5: viên đạn chuyển động với vận tốc 300m/s theo phương ngang thì nổ thành hai mảnh. Mảnh khối lượng 5kg chuyển động với vận tốc 400√3 m/s thẳng đứng lên trên, mảnh thứ hai có khối lượng 15kg. Xác định vận tốc và phương bay của mảnh thứ 2.

v=300m/s; m1=5kg; m2=15kg
v1=400√3m/s; m=m1 + m2=20kg
⃗p=→p1+→p2p→=p1→+p2→
Giải
p2=√p2+p21p2=p2+p12=6928kg.m/s
=> v2=p2m2v2=p2m2= 461 (m/s)
tanα=p1pp1p=> α=300.
Bài tập 6. Một hạt nhân phóng xạ ban đầu đứng yên phân rã thành 3 hạt: electron; nơtrino và hạt nhân con. Động lượng của electron là 9.10-23kg.m/s, động lượng của hạt nơtrino vuông góc với động lượng của electron và có độ lớn 12.10-23kg.m/s. Tìm hướng và độ lớn động lượng của hạt nhân con.
=> hướng của các hạt như hình vẽ
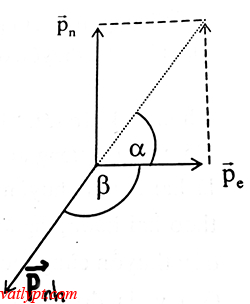
=> pnh2 = pn2 + pe2 => pnh = 15.10-23kg.m/s
tanα = pn/pe = 4/3 => α = 53o
β = 180o – α = 127o
Bài tập 7. Vật khối lượng m1 = 5kg tượt không ma sát theo một mặt phẳng nghiêng, góc nghiêng α = 60o. Từ độ cao h = 1,8m rơi vào một cái xe cát khối lượng m2 = 45kg đang đứng yên. Tìm vận tốc của xe sau đó. Bỏ qua ma sát giữa xe và mặt đường.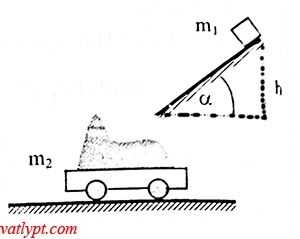
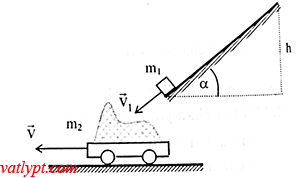
Vận tốc của vật ngay trước khi chạm vào xe cát v1 = √2gh2gh = 6m/s
áp dụng định luật bảo toàn động lượng theo phương ngang
m1v1cosα = (M + m)v => v = 0,3m/s
Bài tập 8. Quả cầu I chuyển động trên mặt phẳng ngang trơn, với vận tốc không đổi đến đập vào quả cầu II đang đứng yên. Va chạm là hoàn toàn đàn hồi. Sau va chạm vận tốc của hai quả cầu ngược nhau, cùng độ lớn. Tính tỉ số các khối lượng của hai quả cầu.
vo là vận tốc của quả cầu I trước va chạm
v1; v2 lần lượt là vận tốc của quả cầu I, II sau va chạm
áp dụng định luật bảo toàn động lượng:
m1vo = m1v1 + m2v2 (1)
v2 = – v1 (2)
áp dụng định luật bảo toàn cơ năng cho va chạm đàn hồi
0,5m1vo2 = 0,5m1v12 + 0,5m2v22 (3)
từ (1) và (2) => m1/m2 = 1/3
Bài tập 9. Quả cầu khối lượng M = 1kg treo ở đầu một dây mảnh nhẹ chiều dài L = 1,5m. Một quả cầu m = 20g bay ngang đến đập vào M với vận tốc v =50m/s. Coi va chạm là hoàn toàn đàn hồi xuyên tâm. Tính góc lệch cực đại của dây treo M.
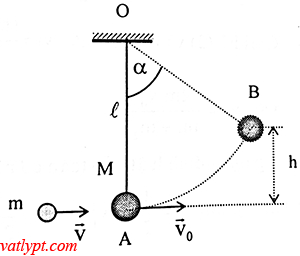
Phương trình bảo toàn động lượng, bảo toàn động năng
mv = mv1 + Mv2 (1)
0,5mv2 = 0,5mv12 + 0,5mv22 (2)
từ (1) và (2) =>
v1 = (m-M)v/(m+M)
v2 = 2mv/(m + M)
áp dụng định luật bảo toàn cơ năng cho vật M tại 2 vị trí A, B gốc thế năng tại A.
0,5Mv2 = mgh = MgL(1-cosα) => α = 29,5o
Bài tập 10. Hai quả cầu m1 = 200g, m2 = 100g treo cạnh nhau bởi hai dây song song bằng nhau. Nâng quả cầu I lên độcao h = 4,5cm rồi buông tay. Hỏi sau va chạm, các quả cầu được nâng lên độ cao bao nhiêu nếu va chạm là hoàn toàn đàn hồi.
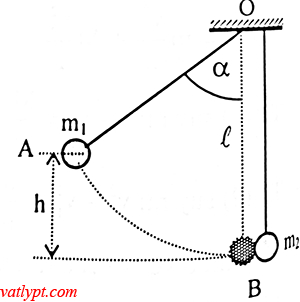
Gọi vo là vận tốc của vật m1 trước va chạm. Áp dụng định luật bảo toàn cơ năng cho vật m1 tại hai vị trí A và B gốc thế năng tại B =>
m1gh = 0,5m1vo2 => vo2 = 2gh
Gọi v1; v2 lần lượt là vận tốc của vật m1 và m2 ngay sau va chạm =>
m1vo = m1v1 + m2v2 (1)
0,5m1vo2 = 0,5m1v12 + 0,5m2v22 (2)
từ (1) và (2) => v1 = (m1 – m2)vo/(m1 + m2)
v2 = 2m1vo/(m1 + m2)
Áp dụng bảo toàn cơ năng cho mỗi vật
m1gh1 = 0,5m1v12 => h1 = v12/2g = 0,5cm
m2gh2 = 0,5m2v22 => h2 = v22/2g = 8cm.
Bài tập 11. Hai quả cầu giống nhau treo cạnh nhau bởi hai dây song song bằng nhau. Kéo lệch hai quả cầu khỏi phương thẳng đứng về hai phía với cùng góc α rồi thả cùng lúc. Coi va chạm giữa hai quả cầu là hoàn toàn đàn hồi. Tính lực tác dụng lên giá treo.a/ Tại lúc bắt đầu thả các quả cầu.b/ Tại thời điểm đầu, cuối của quá trình va chạm giữa các quả cầu.c/ Tại thời điểm quả cầu bị bị dạng nhiều nhất.
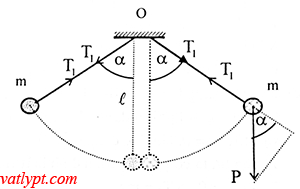
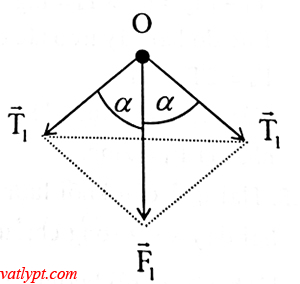
a/ T1 = mgcosα => F1 = 2T1cosα = 2mgcos2α
b/ Tại thời điểm đầu của quá trình va chạm 2 quả cầu ở vị trí cân bằng
Gọi lực căng của mỗi dây treo lúc này là T2, vận tốc của mỗi quả cầu là v2.
Áp dụng định luật bảo toàn cơ năng cho mỗi quả cầu
mgL(1-cosα) = 0,5mv22 => v22 = 2gL(1-cosα)
áp dụng định luật II Newton
T2 – mg = maht = mv22/L => T2 = mg + mv22/L = mg(3 – 2cosα)
F2 = 2T2 = 2mg(3-2cosα)
Tại thời điểm cuối của quá trình va chạm:
Gọi lực căng dây treo lúc này là T3 vận tốc của mỗi quả cầu là v3. Do va chạm đàn hồi xuyên tâm và hai quả cầu giống nhau nên sau va chạm hai quả cầu đổi vận tốc cho nhau. Có nghĩa là hai quả cầu đổi chiều chuyển động nhưng độ lớn vận tốc không đổi => T3 = T2 => F3 = F2
c/ Các quả cầu bị biến dạng nhiều nhất khi chúng đi qua vị trí cân bằng và có vận tốc v4 = 0.
Gọi lực căng mỗi dây lúc này là T4 => T4 = mg => F4 =2T4 = 2mg.
Bài tập 12. Hai quả cầu khối lượng m và km treo cạnh nhau trên hai dây song song có chiều dài L1 và L2(L1>L2). kéo dây treo m lệch góc α rồi buông tay. Tìm góc lệch cực đại của hai dây treo sau va chạm lần I. Coi va chạm là tuyệt đối đàn hồi.
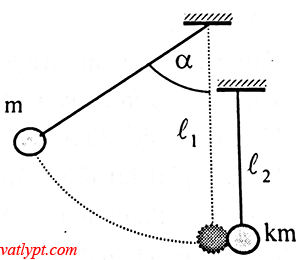
mgL1(1 – cosα) = 0,5mvo2 => vo2 = 2gL1(1-cosα)
Gọi v1; v2 lần lượt là vận tốc của vật m và vật km ngay sau va chạm. Vì va cạm là đàn hồi xuyên tâm nên ta có:
v1 = (m-km)vo/(m + km) = (1-k)vo/(1+k)
v2 = 2mvo/(m + km) = 2vo/(1 + k)
Áp dụng định luật bảo toàn cơ năng cho mỗi vật
vật m: 0,5mv12 = mgL1(1-cosα1)
=> cosα1 = 1 – (1−k1+k)2(1−k1+k)2(1 – cosα)
vật km: 0,5kmv22 = mgL2(1-cosα2)
=> cosα2 = 1 – 4L1L2(1+k)24L1L2(1+k)2(1-cosα)
Bài tập 13. Vật khối lượng m1 được thả không vận tốc đầu và trượt xuống một vòng xiếc bán kính R. Tại điểm thấp nhất nó va chạm đàn hồi với vật m2 đang đứng yên. Sau va chạm m2 trượt theo vòng xiếc đến độ cao h thì rời khỏi vòng xiếc (h > R). Vật m1 giật lùi lên mang nghiêng rồi lại trượt xuống độ cao h của vòng xiếc thì cũng rời vòng xiếc. Tính độ cao ban đầu H của m1 và tỉ số các khối lượng. Bỏ qua ma sát.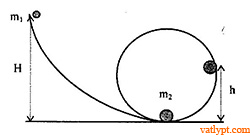

Bài tập 14. Ba vật khối lượng m1; m2; m3 có thể trượt không ma sát theo trục nằm ngang (hình vẽ). và m1; m3>> m2. Ban đầu m1, m3 đứng yên còn m2 có vận tốc v. Va chạm hoàn toàn đàn hồi. Tìm vận tốc cực đại của m1; m3 sau va chạm.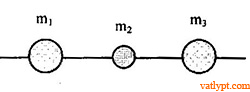
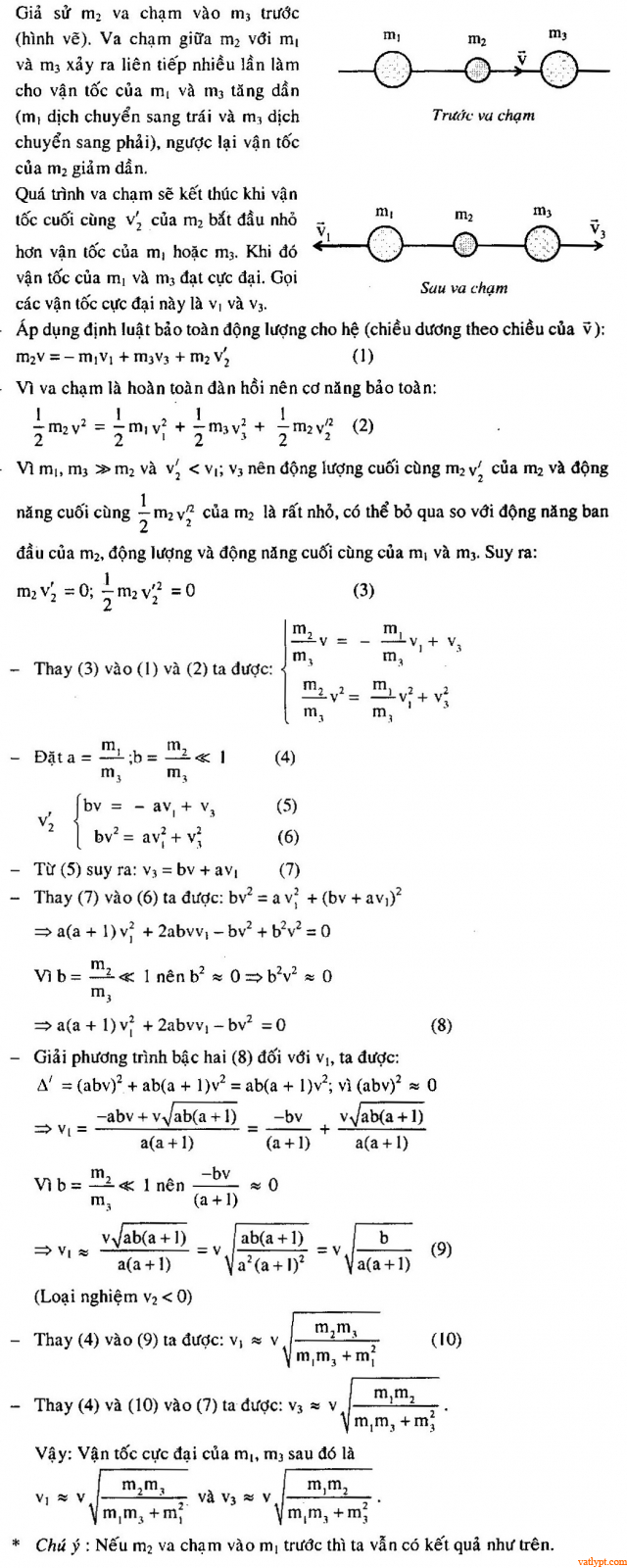
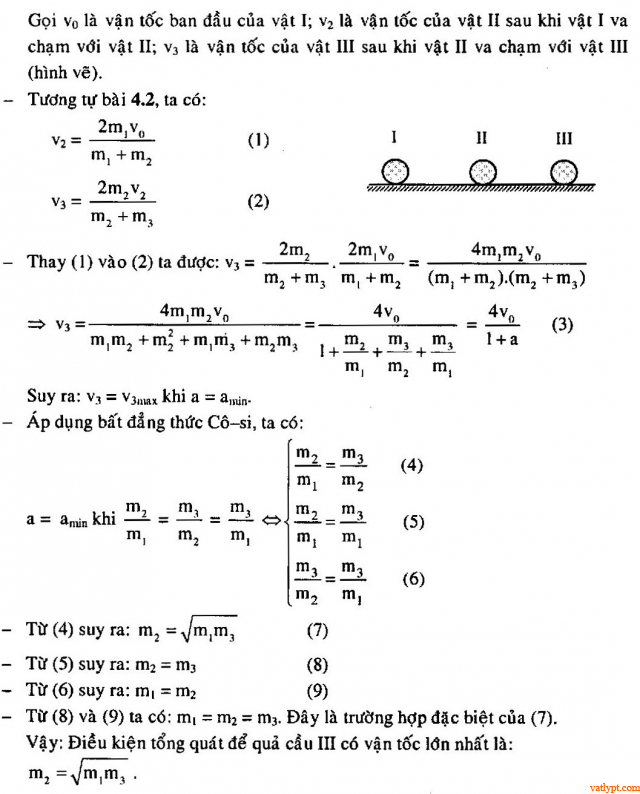
Bài tập 15. Ba quả cầu khối lượng m1; m2; m3 đặt thẳng hàng trên sàn trơn. Quả cầu I chuyển động đến quả cầu II với vận tốc nào đó còn quả cầu II và III đang đứng yên (hình vẽ). Tính m2 theo m1 và m3 để sau va chạm (tuyệt đối đàn hồi) quả cầu III có vận tốc lớn nhất.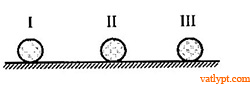
Bài tập 16. Cho hệ như hình vẽ. Hai vật cùng khối lượng m đặt trên sàn nằm ngang và nối với nhau bằng lò xo độ cứng k. Vật thứ ba cùng khối lượng m đến đập vào một trong hai vật với vận tốc v dọc theo phương song song với trục lò xo. Coi va chạm là tuyệt đối đàn hồi.a/ Chứng minh rằng hai vật nối bằng lò xo luôn chuyển động cùng hướng.b/Tính vận tốc mỗi vật khi lò xo dãn tối đa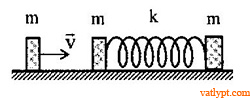

Bài tập 17. Một viên đạn khối lượng m1 = 1kg bay với vận tốc v1 = 100m/s đến cắm vào một toa xe chỏ cát có khối lượng m2 = 1000kg đang chuyển động với vận tốc v2 = 10m/s. Tính nhiệt lượng tỏa ra trong hai trường hợpa/ xe chuyển động cùng chiều đạnb/ xe và đạn chuyển động ngược chiều.

Bài tập 18. Búa máy khối lượng m1 = 1000kg rơi từ độ cao 3,2m vào một cái cọc khối lượng m2, va chạm là mềm. Tính- vận tốc của búa và cọc sau va chạm- tỉ số phần trăm giữa nhiệt tóa ra và động năng của búa trước va chạmxét hai trường hợpa/ m2 = 100kgb/ m2 = 5000kg

Bài tập 19. Hai quả cầu nhỏ nối với nhau bằng sợi dây ngắn thẳng đứng. Quả cầu ở trên được truyền vận tốc v hướng lên. Hệ sẽ đạt độ cao cực đại bao nhiêu. Biết tương tác giữa hai quả cầu khi dây bị căng ra giống như va chạm mềm.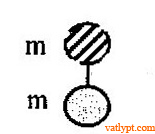



Bài tập 21. Đĩa cân của một cân lò xo có khối lượng m1 = 120g, lò xo có độ cứng k = 20N/m. Vật khối lượng m = 60g rơi xuống từ độ cao h = 8cm so với đĩa, không vận tốc đầu. Coi va chạm là hoàn toàn không đàn hồi. Hỏi vật đã dời xa nhất đến đâu so với vị trí ban đầu? bỏ qua sức cản của không khí.

Bài tập 22. Vật nặng củabúa máy có trọng lượng P1 = 900N được dùng để đóng một chiếc cọc P2 = 300N vào đất. Mỗi lần đóng cọc nún sâu h = 5cm.
a/ Búa rơi từ độ cao H = 2m xuống đầu cọc và lực cản của không khí vào búa khi rơi F = 0,1P1. Coi va chạm là tuyệt đối không đàn hồi. Tính lực cản của đất.
b/ Tính phần trăm năng lượng của búa bị tiêu hao để làm nóng và biến dạng trong các va chạm giữa búa và cọc.
c/ Tính phần trăm năng lượng của búa bị tiêu hao để thắng lực cản của đất.

Bài tập 23. Hòn bi thép khối lượng M và hòn bi sáp khối lượng m treo cạnh nhau ở đầu hai sợi dây song song bằng nhau. Kéo dây treo M lệch góc α rồi buông tay, sau va chạm (tuyệt đối không đàn hồi) góc lệch cực đại của hai dây treo là β. Tìm khối lượng hòn bi sáp và độ tiêu hao cơ năng của hệ. Bỏ qua sức cản của không khí.

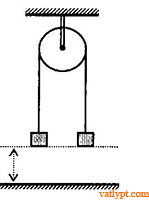
Bài tập 24. Cho hệ như hình vẽ. Cho biết m1 = 2kg, m2 = 3kg, vo = 0 ban đầu m1; m2 cách mặt đất 1m. Coi va chạm giữa m2 với đất và tương tác giữa m1 và m2 khi dây bắt đầu căng là va chạm mềm. a/ Trong quá trình chuyển động, m1 có thể đi xuống cách mặt đất một khoảng thấp nhất là bao nhiêu.
b/ khi m1 ở vị trí thấp nhất trong câu a, tính lượng cơ năng đã biến thành nội năng của m1; m2, đất.
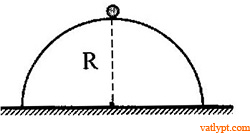
Bài tập 25. Vật nhỏ trượt không ma sát với vo = 0 từ đỉnh bán cầu bán kính R đặt cố định trên sàn ngang. Đến một nơi nào đó trên bán cầu, vật rời bán cầu rơi xuống sàn và nẩy lên (hình vẽ). Biết va chạm của vật với sàn là hoàn toàn đàn hồi. Tìm độ cao H mà vật đạt tới sau va chạm.

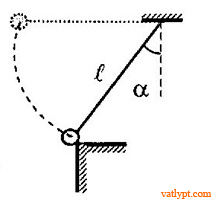
Bài tập 26. Hòn bi sắt treo vào dây chiều dài l = 1,2m được keo cho dây nằm ngang rồi thả rơi Khi dây hợp góc α = 30o với đường thẳng đứng, bi va chạm đàn hồi với bề mặt thẳng đưungs của một tấm sắt lớn cố định (hình vẽ). Hỏi bi sẽ nảy lên đến độ cao bao nhiêu?

Bài tập 27. Thang máy lên cao với gia tốc a, vận tốc ban đầu vo = 0. Từ độ cao H so với sàn, ngay khi thang máy bắt đầu chuyển động, người ta thả một quả cầu. Sau t giây, gia tốc thang máy đổi chiều và triệt tiêu sau t giây nữa, sau đó quả cầu va chạm với sàn thang máy.
Tìm độ cao h (so với sàn thang máy) mà quả cầu đạt tới sau va chạm

Bài tập 28. Một hòn bi được thả rơi với vo = 0 từ độ cao ho = 5m. Khi chạm đất bị mất 1/2 động năng và nảy lên thẳng đứng.
a/ Tính độ cao bi nảy lên sau va chạm thứ 1, 2, … n
b/ Tính đoạn đường tổng cộng bị vạch được cho đến lúc dừng.
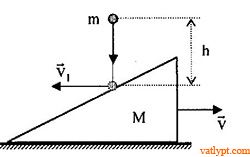
Bài tập 29. Quả cầu khối lượng m rơi từ độ cao h xuống, đập vào mặt phẳng nghiêng một cái nêm khối lượng M đứng yên trên sàn nhẵn. Sau va chạm tuyệt đối đàn hồi đạn nảy ra theo phương ngang còn nêm chuyển động với vận tốc v (hình vẽ). Tính v.

Bài tập 30. Viên đạn khối lượng m bay theo phương ngang với vận tốc v1 và đâm xuyên qua ột quả cầu khối lượng M đặt trên sàn nhẵn. Sau khi xuyên qua M, m chuyển động theo chiều cũ với vận tốc v2. Tìm nhiệt lượng tỏa ra trong quá trình trên.

Bài tập 31. Đạn khối lượng m1 = 9g bay với vận tốc vo = 160m/s theo hướng hợp với phương ngang góc α = 30o, xuyên qua giữa một bệ ván m2 = 0,3kg. sau đó đạn lên đến độ cao cực đại H = 45m tính từ vị trí ban đầu của bệ ván. Hỏi tấm ván sẽ được nâng lên độ cao nào? Bỏ qua sức cản của không khí, coi lực tương tác giữa vật và bệ ván là rất lớn.
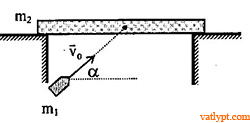

Bài tập 32. Bản khối lượng M treo ở đầu một dây dài. Đạn khối lượng m bay theo phương ngang đến đập vuông góc vào mặt bàn. Nếu đạn có vận tốc vo, bó dừng lại ở mặt sau của bản. Tìm vận tốc bản sau khi đạn có vận tốc v1 và bay xuyên qua bản (v1 > vo).
Coi ma sát giữa đạn và bản không phụ thuộc vào vận tốc đạn.

Bài tập 33. Hai quả cầu nhỏ A, B có khối lượng lần lượt là m1 = 100g, m2 = 200g treo sát nhau bởi hai dây song song có cùng chiều dài l = 1m. Kéo A lên đến vị trí dây treo nghiêng góc α = 60o với phương thẳng đứng rồi buông tay.
a/ Tính vận tốc B sau va chạm và độ cao B đạt tới. Biết sau va chạm (xuyên tâm) A dừng lại
b/ Va chạm trên có là hoàn toàn đàn hồi không tại sao? tính vận tốc A, B sau va chạm nếu va chạm là hoàn toàn đàn hồi.

Bài tập 34. Hai quả cầu khối lượng M và m treo cạnh nhau bằng các dây song song dài bằng nhau. Kéo M để dây treo lệch góc α rồi thả ra. Sau va chạm vật M dừng lại còn m đi lên, dây treo lệch góc tối đa β. Hỏi sau va chạm lần II, dây treo M sẽ lệch góc cực đại bằng bao nhiêu. Biết trong mỗi lần va chạm, có cùng một tỉ lệ thế năng biến dạng cực đại của các quả cầu chuyển thành nhiệt.
Bài tập 35. Quả cầu khối lượng m1 chuyển động với vận tốc v1 gặp quả cầu đứng yên m2 sao cho khi va chạm vận tốc →v1v1→ hợp với đường nối hai tâm một góc α. Tính vận tốc quả cầu m1 sau va chạm biết va chạm là tuyệt đối không đàn hồi.

Bài tập 36. Vòng tròn bán kính R lăn với vận tốc v trên mặt phẳng ngang đến va chạm hoàn toàn không đàn hồi với một cái bậc có độ cao h < R (hình vẽ). Hỏi ngay sau khi nhảy lên bậc, vòng có vận tốc bao nhiêu. Tính v cực tiểu để vòng có thể nhảy lên khỏi bậc.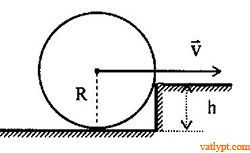

Bài tập 37. Một vật được ném từ mặt đất với vận tốc đầu vo nghiêng góc α với phương ngang. Cách điểm ném một khoảng L có một tấm thép thẳng đứng. Mặt phẳng quỹ đạo của vật vuông góc với tấm thép. Vật va chạm đàn hồi với tấm thép.a/ Điểm rơi của vật cách tấm thép là bao nhiêu.b/ Nếu tấm thép chuyển động với vận tốc bằng u về phía vật và sau va chạm vật rơi trở lại đúng điểm ném thì thời gian từ lúc ném đến lúc va chạm bằng bao nhiêu.

Bài tập 38. Một quả cầu chuyển động trong một hộp vuông, va chạm đàn hồi với đáy và thành của hộp theo một quỹ đạo duy nhất (hình vẽ). Khoảng thời gian giữa va chạm với đáy và với thành là Δt. Đáy hộp nghiêng góc α với phương ngang.Tìm vận tốc của quả cầu ngay sau va chạm.

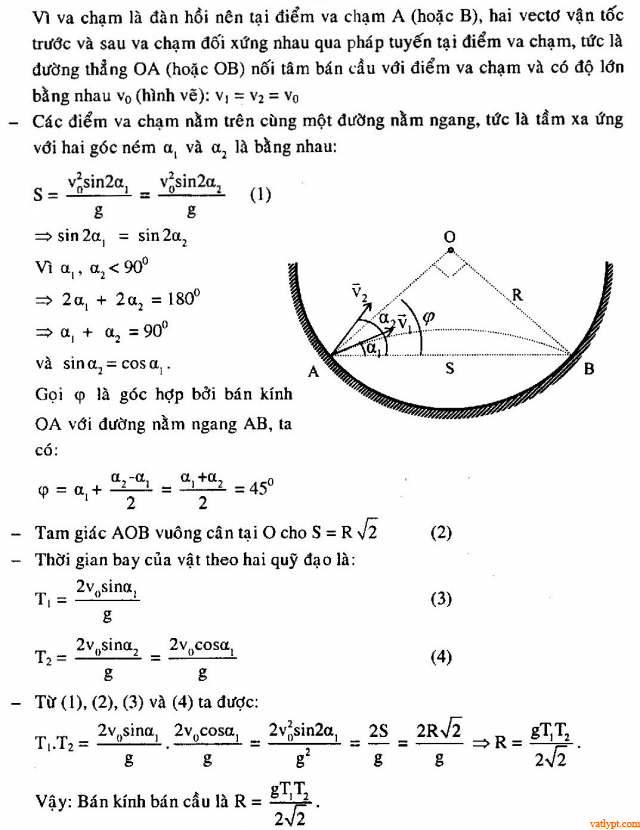
Bài tập 39. Một quả cầu nhảy trong một bán cầu như hình vẽ. Nó va chạm đàn hồi với mặt trong của bán cầu tại hai điểm cùng nằm trên đường nằm ngang (cùng độ cao). Khoảng thời gian chuyển động từ trái sang phải là T1, từ phải sang trái là T2 (T2 ≠ T1). Tìm bán kính bán cầu.