Chương IV: Bài tập bảo toàn năng lượng
Bài tập bảo toàn năng lượng, định luật bảo toàn năng lượng, vật lý 10 chương các định luật bảo toàn.
I/ Tóa tắt lý thuyết
II/ Bài tập bảo toàn năng lượng, định luật bảo toàn năng lượng, vật lý 10 chương các định luật bảo toàn.
Bài tập 1. Một trạm thủy điện hoạt động nhờ một thác nước cao 5m, lưu lượng 20lít/giây. Công suất do máy phát ra là 800W. Tính hiệu suất của trạm thủy điện.
L = 20 lít/giây => m = Lt = 20lít = 20kg ; Pi = 800W
Ptp = A/t = mgh = 20.10.5 (W)
Hiệu suất: H = Pi/Ptp = 0,8 = 80%
Bài tập 2. Búa máy khối lượng 500kg rơi từ độ cao 2m và đóng vào cọc làm cộc ngập thêm vào đất 0,1m. Lực đóng cọc trung bình là 80000N. Tính hiệu suất của búa máy.
Công có ích: Ai = Ftb.s
Hiệu suất H = Ai/Atp = 0,8 = 80%
Bài tập 3. Một lò xo có chiều dài tự nhiên 15cm. Lò xo được nén lại còn 5cm. Độ cứng của lò xo 100N/m.
a/ Một viên bi khối lượng 40g dùng làm đạn được cho tiếp xúc với lò xo bị nén. Khi bắn, lò xo truyền toàn bộ thế năng cho đạn. Tính vận tốc lúc bắn.
b/ Đạn bắn theo phương nằm ngang và lăn trên một mặt ngang nhẵn, sau đó lên một mặt nghiêng góc nghiêng α = 30o. Tính chiều dài lớn nhất mà đạn lăn được trên mặt phẳng nghiêng, nếu bỏ qua ma sát trên mặt phẳng nghiêng.
c/ Máng nghiêng có ma sát đạn lăn được 1/2 chiều dài của máng nghiêng tính hệ số ma sát của máng nghiêng.
a/ Bảo toàn cơ năng: 0,5kx2 = 0,5mvo2 => vo = 5m/s
b/ Chiều dài lớn nhất mà vật lăn lên được trên mặt phẳng nghiêng (không có ma sát)
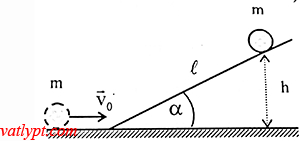
0,5mvo2 = mgh = mgL.sinα => L = 2,5m
c/ Áp dụng bảo toàn năng lượng
ΔW = AFms => mgL’sinα – 0,5mvo2 = -µ(mgcosα).L’ => µ = 0,58
với L’ = L/2
Chương IV: Bài tập bảo toàn năng lượng
Bài tập 4. Một vật nhỏ tại D được truyền vận tốc đầu vo theo hướng DC (hình vẽ). Biết vật đến A thì dừng lại, AB = 1m, BD = 20m, hệ số ma sát µ = 0,2. Tính vo.
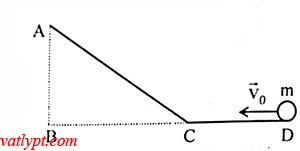
AFms = AFms1 + AFms2 = -µmg.DC – µ.(mgcosα).CA
Áp dụng định luật bảo toàn năng lượng
=> AFms = ΔW = mgAB – 0,5mvo2 => vo = 10m/s
Bài tập 5. Một chiếc xe tắt máy thả lăn không vận tốc ban đầu từ A xuống dốc AC và chạy đến D thì dừng lại. Từ D xe mở máy và chạy ngược lại theo chiều đường DCA và dừng lại khi lên đến A. Tính công của lực kéo của động cơ biết AB = 10m, khối lượng xe 500kg.

áp dụng định luật bảo toàn cơ năng => AFms = ΔW = -mgAB
khi xe đi lên theo định luật bảo toàn năng lượng thì tổng công của lực ma sát và lực kéo của động cơ (đều không phải là lực thế) bằng độ biến thiên cơ năng của xe
AFms + AF = ΔW2 => AF = ΔW2 – AFms = mgAB – 0 – (-mgAB) = 2mgAB = 100kJ
Bài tập 6. Vật 1kg ở độ cao h = 24m được ném theo phương thẳng đứng xuống dưới với vận tốc vo = 14m/s. Khi chạm đất, vật đào sâu xuống một đoạn s = 0,2m. Bỏ qua lực cản của không khí. Tính lực cản trung bình của đất.
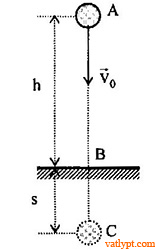
AFc = -Fcs
WC = -mgs
WA = mgh + 0,5mv2
Bảo toàn năng lượng
AFc = ΔW = -mgs – (mgh + 0,5mvo2) => Fc = 1700N
Bài tập 7. Quả cầu khối lượng m treo dưới một dây chiều dài L. Nâng quả cầu lên để dây treo nằm ngang rồi buông tay. Biết vận tốc của quả cầu ở vị trí cân bằng là v. Tìm lực cản trung bình của không khí lên quả cầu.
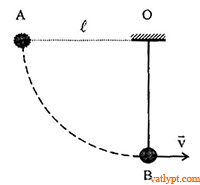
AC = WB – WA => -FC.s = (0,5mv2 – mgL)
=> -FC(2πL/4) = (0,5mv2 – mgL) => FC = (m/π)(2g – v2/L)
Bài tập 8. Hai bình hình trụ giống nhau được nối với nhau bằng ống có khóa. Ban đầu khóa đóng và hình bên trái có mộtkhối nước khối lượng m, mặt thoáng ở độ cao h. Mở khóa cho hai bình thông nhau và mạt thoáng ở hai bình có độ cao h/2 (bỏ qua thể tích của ống thông). Tìm độ biến thiên thế năng của khối nước. Cho biết sự chuyển hóa năng lượng trong hiện tượng trên.
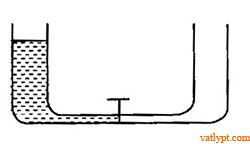
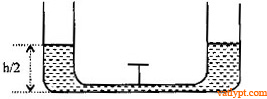
– khi cân bằng mặt thoáng của hai bình có độ cao bằng nhau và bằng h/2
– Coi khối nước trong mỗi bình như một chất điểm có khối lượng bằng khối lượng của khối nước đặt tại khối tâm của mỗi khối, tức là độ cao bằng h/4
– Độ biến thiên thế năng của khối nước
ΔWt = mgh/4 – mgh/2 = -mgh/4 < 0 => thế năng của khối nước giảm => một phần thế năng của khối nước đã chuyển hóa thành nhiệt làm nóng khối nước và thành bình.
Bài tập 9. Cho hệ như hình vẽ α = 30o, m1 = 150g; m2 = 100g, hệ chuyển động không vận tốc ban đầu. Hệ số ma sát giữa m1 và mặt phẳng nghiêng là µ = 0,15. Dùng định luật bảo toàn năng lượng tính gia tốc của mỗi vật suy ra vận tốc của mỗi vật sau khi chuyển động một thời gian t = 4s.
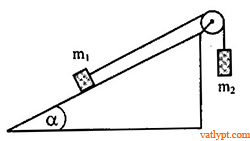
Dây không dãn nên gia tốc của hai vật bằng nhau => quãng đường 2 vật chuyển động được bằng nhau..
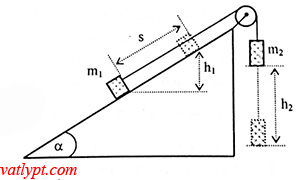
giả sử m2 đi xuống, m1 đi lên. Khi m2 đi xuống thẳng đứng quãng đường s thì m1 đi lên cùng quãng đường s trên mặt phẳng nghiêng => h2 = -s và h1 = s.sinα (1)
AFms = -µ(mgcosα).s (2)
Áp dụng bảo toàn năng lượng
AFms = ΔW = m1gh1 + m2gh2 + 0,5(m1+m2)v2 (3)
từ (1) (2) và (3) => v2 => a = v2/2s = 0,22m/s2
vận tốc của mỗi vật v = at = 0,88m/s2
Bài tập 10. Vật trượt không vận tốc đầu xuống theo một mặt phẳng nghiêng góc α = 45o. Ở chân mặt phẳng nghiêng vật va chạm với một tường chắn vuông góc với hướng chuyển động khiến vận tốc vật đổi chiều nhưng giữ nguyên độ lớn. Sau đó vật đi lên trên mặt phẳng được một nửa độ cao ban đầu. Tính hệ số ma sát giữa vật và mặt phẳng nghiêng.
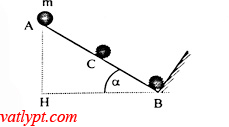
AFms = -µmg(cosα)(AB + BC) = -µmg(HB/AB).3AB/2 = -µmg3HB/2
HB = AH/tanα => AFms = -µmg3AH/(2tanα)
ΔW = WC – WA = mgAH/2 – mgAH = -mgAH/2
bảo toàn năng lượng AFms= ΔW => µ = 0,33
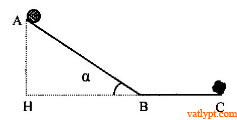
Bài tập 11. Một vật trượt không vận tốc đầu xuống mặt phẳng nghiêng AB rồi tiếp tục đi thêm một đoạn BC trên mặt phẳng ngang (hình vẽ). Biết AH = h, BH = l, BC = x, hệ số ma sát trên cả hai đoạn đường là µ. Dùng định luật bảo toàn năng lượng tính x. Cho biết điều kiện để bài toán có nghiệm.

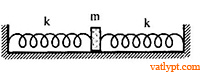
Bài tập 12. Vật m = 0,5kg gắn vào các vách thẳng đứng bởi hai lò xo giống nhau và chuyển động theo phương dọc theo hai lò xo (hình vẽ). Tại một thời điểm nào đó, độ lệch cực đại liên tiếp của vật khỏi vị trí cân bằng bên phải và bên tái là s1 = 10cm; s2 = 7cm. Biết độ cứng của mỗi lò xo là k = 15N/m. Tìm hệ số ma sát µ giữa vật và mặt phẳng.

Bài tập 13. Vật m = 1kg đặt trên sàn xe nằm ngang đứng yên thì được truyền vận tốc vo = 10m/s. Xe khối lượng M = 100kg và có thể chuyển động trên mặt phẳng ngang nhẵn. Do ma sát, vật chuyển động một đoạn trên sàn xe rồi dừng lại. Tính nhiệt lượng tỏa ra trong quá trình vật chuyển động đối với xe.

Bài tập 14. Trên mặt bàn nhẵn nằm ngang có hai khối hộp giống nhau, nối với nhau bằng một lò xo độ cứng k. Chiều dài lò xo ở trạng thái chưa biến dạng là lo. Tác dụng lực F không đổi nằm ngang dọc theo lò xo vào khối hộp bên trái. Tìm khoản cách cực đại và cực tiểu giữa các khối hộp khi hệ chuyển động.

