Chương III: Bài tập hợp lực song song cùng chiều, ngẫu lực
Chương III: Bài tập cân bằng tổng quát của vật rắn
Bài tập hợp lực song song cùng chiều, ngẫu lực. Các dạng bài tập hợp lực song song cùng chiều, ngẫu lực. Phương pháp giải Bài tập hợp lực song song cùng chiều, ngẫu lực chương trình vật lý lớp 10 cơ bản, nâng cao.
I/ Tóm tắt lý thuyết
Bài tập hợp lực song song cùng chiều, ngẫu lực
Bài tập 1. Đòn gánh dài 1,5 m. Hỏi vai người gánh hàng phải đặt ở điểm nào để đòn gánh cân bằng và vai chịu tác dụng của một lực bằng bao nhiêu? biết hai đầu đòn gánh là thùng gạo và thùng ngô có khối lượng lần lượt là 30kg và 20kg, bỏ qua khối lượng của đòn gánh, lấy g=10m/s2.
d1 + d2=1,5m
m1=30kg; m2=20kg
Giải
F1=m1g=300N; F2=m2g=200N
F=F1 + F2=500N
F1d1=F2d2 (1)
d1 + d2=1,5 (2)
từ (1) và (2) => d1=0,6m; d2=0,9m
Bài tập 2. Hai lực song song cùng chiều, một lực có độ lớn 13N cách lực kia 0,2m và cách giá của hợp lực 0,12m. Tính độ lớn của lực còn lại và hợp lực.
F1=13 N; d1=0,12 m; d2=0,2 – 0,12=0,08 (m);
Giải
F1d1=F2.d2 => F2=19,5N
F=F1 + F2=32,5 N.
Bài tập 3. Hai người khiêng vật nặng 100kg bằng một đòn gánh dài 1m, biết điểm treo vật cách vai người thứ nhất 60cm. Tính lực tác lên vai của mỗi người, lấy g=10m/s2 bỏ qua khối lượng của đòn gánh.
m=100kg => F=mg=1000N
d1=0,6m => d2=0,4m
Giải
F1 + F2=1000 (1)
F1d1=F2d2 (2)
Từ (1) và (2) => F1=400N; F2=600N
Bài tập 4. Thanh rắn mỏng phẳng đồng chất trục quay đi qua trọng tâm của thanh. Tác dụng vào hai điểm A,B của thanh rắn cách nhau 4,5cm ngẫu lực có độ lớn 5N. Tính Momen của ngẫu lực trong các trường hợp sau
a/ Thanh rắn đang ở vị trí thẳng đứng
b/ Thanh rắn đang ở vị trí hợp với phương thẳng đứng góc 30o.

F=5N
a/ d1=AB=4,5cm
b/ d2=ABcos30
Giải
a/ M=F.d1=0,225 N.m.
b/ M=F.d2=0,195 Nm.
Bài tập 5. Một vật rắn phẳng, mỏng có dạng là một tam giác đều ABC, mỗi cạnh là a=20 cm. Người ta tác dụng vào vật một ngẫu lực nằm trong mặt phẳng của tam giác. Các lực có độ lớn là 8 N và đặt vào hai đỉnh A và B. Tính mômen của ngẫu lực trong các trường hợp sau đây:
a) Các lực vuông góc với cạnh AB.
b) Các lực vuông góc với cạnh AC.
c) Các lực song song với cạnh AC.

Giải
a) M=F.AB=1,6 N.m.
b) M=F.AH=F. AC2AC2=0,8 N.m.
c) M=F.BH=F.AB.cos300=1,4 N.m.
Bài tập 6. Một bàn vuông nhẹ có bốn chân giốngnhau. Nếu đặt vật có trọng lượng quá 2P ở đúng giữa bàn thì chân bàn gãy. Tìm các điểm có thể đặt vật trọng lượng P mà chân bàn không gãy.
pmax = 2P/4 = P/2
Vì bốn chân bàn giống nhau => chỉ cần xét điều kiện cho 1 chân
Vị trí các chân bàn như hình vẽ, đặt vật tại điểm M (x,y)
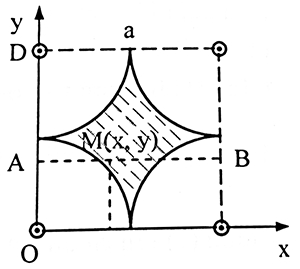
Áp dụng qui tắc hợp lực song song cùng chiều
Tại điểm A(0,y) và điểm B(a,y): FA + FB = P và FA/FB = MB/MA = (a-x)/x
=> FA/P = (a-x)/a => FA = P(a-x)/a (1)
Phân tích lực FA thành hai lực F1 và F2 đặt vào hai chân bàn
F1 + F2 = FA; F1/F2 = AD/AO = (a-y)/y
=> F1/FA = (a-y)/a => F1 = FA(a-y)/a (2)
Thay (2) vào (1) => F1 = P(a-x)(a-y)/a2
Để chân bàn không gãy F1 ≤ P/2 => (a-x)(a-y) ≤ a2/2 => y ≥ a – a2/2(a-x)
y = a – a2/2(a-x) là đường hypebol đi qua trung điểm cả hai cạnh tương tự với các chân bàn còn lại => để chân bàn không gãy phải đặt P trong vùng gạch chéo như hình vẽ.
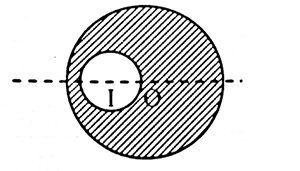
Bài tập 7. Xác định vị trí trọng tâm của bản mỏng là đĩa tròn tâm O bán kính R, bản bị khoét một lỗ tròn nhỏ bán kính R/2 như hình vẽ
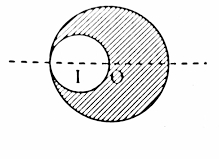
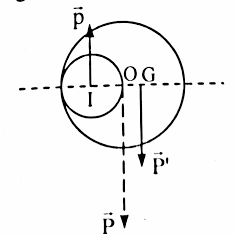
Khi đĩa chưa bị khoét, trọng tâm đĩa nằm tại O; lỗ tròn bị khoét có trọng tâm nằm tại I.
Gọi P là trọng lượng của đĩa chưa khoét, p là trọng lượng lỗ tròn bị khoét, P’ là trọng lượng của đĩa bị khoét => P’ = P – p
Theo qui tắc hợp lực song song ngược chiều ta có:
IG/OG = P/p = M/m = πR2D/[π(R/2)2D] = 4
Trong đó D là khối lượng riêng của đĩa tròn.
=> IO + OG = 4OG => OG = IO/3 = R/6
=> Trọng tập G của đĩa bị khoét cách O một đoạn OG = R/6
Bài tập 8. Xác định trọng tâm của bản mỏng là đĩa tròn tâm O bán kính R, bản bị khoét một lỗ tròn bán kính r > R/2 và có tâm I cách O đoạn R/2
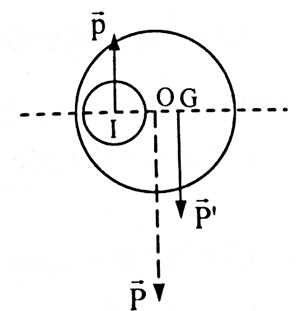
Tương tự bài 7 ta có
IG/OG = M/m = πR2.D/(π.r2D) = R2/r2
IG = IO + OG = R/2 + OG
=> (R/2 + OG)/OG = R2/r2 => OG = R.r2/2(R2 – r2)
Vậy trọng tâm của đĩa bị khoét cách O một đoạn OG = R.r2/2(R2 – r2)
Bài tập 9. Một bản mỏng phẳng đồng chất, bề dày đều có dạng như hình vẽ. Xác định vị trí trọng tâm của bản. (phần mầu trắng là phần bị khoét đi)
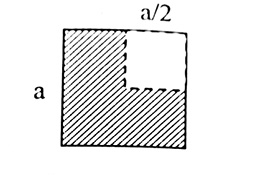
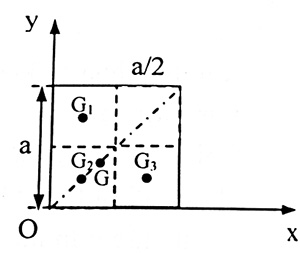
Áp dụng phương pháp tọa độ ta có
XG = (m1XG1 + m2XG2 + m3XG3)/(m1 + m2 + m3)
=> XG = m(a/4 + a/4 + 3a/4)/3m = 5a/12
YG = (m1YG1 + m2YG2 + m3YG3)/(m1 + m2 + m3)
=> YG = m(a/4 + a/4 + 3a/4)/3m = 5a/12
=> trọng tâm của bản tại điểm có tọa độ G(5a/12; 5a/12)
Bài tập 10. thanh AB trọng lượng P1 = 100N, chiều dài L = 1m, trọng lượng vật nặng P2 = 200N tại C, AC = 60cm.
a/ Tính hợp lực của P1 và P2
b/ Tìm lực nén lên hai giá đỡ ở hai đầu thanh
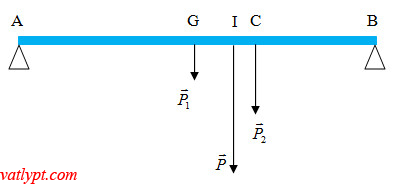
a/Thanh AB đồng chất => trọng tâm G nằm tại điểm chính giữa thanh =>
AG = GB = AB/2
Gọi I là điểm đặt của hợp lực P1; P2 => theo qui tắc hợp lực song song cùng chiều
P = P1 + P2 = 300N
P2/P1 = IG/IC = 2 => IG = 2IC
IG + IC = GC => 3IG = AC – AG = 10cm => IG = 6,67cm; IC = 3,33cm
b/ Gọi N1; N2 là lực nén của thanh lên hai điểm A, B
N1 + N2 = P = 300N (1)
N2/N1 = AI/BI (2)
từ (1) và (2) => N1 = 170N; N2 = 130N
Bài tập 11. Hệ số ma sát µ giữa bánh xe phát động của ô tô và mặt đường phải có giá trị nhỏ nhất bao nhiêu để ô tô khối lượng 2 tấn chở 4 tấn hàng có thể chuyển động với gia tốc a = 0,2m/s2. Biết chỉ có bánh sau là bánh phát động và coi khối tâm của ô tô nằm giữa khoảng cách hai trục bánh, khối tâm của hàng nằm trên trục sau.
Các lực tác dụng vào ô tô: Trọng lực P, phản lực Q, lực phát động F
theo định luật II newtơn: F = (m1 + m2)a
Với F ≤ Fmsn = µ(N1 + N2)
N2 = m2g: áp lực của hàng lên bánh phát động
N1: áp lực của xe lên các bánh
áp dụng qui tắc hợp lực song song cùng chiều => N1 = P1/2 = m1g/2 phát động
=> (m1 + m2)a ≤ µ(N1 + N2) => µ ≥ 0,024
Bài tập 12. Thanh nhẹ AB nằm ngang chiều dài L = 1m, chịu tác dụng của ba lực song song cùng chiều và vuông góc với thanh. F1 = 20N; F3 = 50N ở hai đầu thanh và F2 = 30N ở chính giữa thanh
a/ Tìm độ lớn và điểm đặt của hợp lực
b/ Suy ra vị trí đặt giá đỡ để thanh cân bằng và lực nén lên giá đỡ
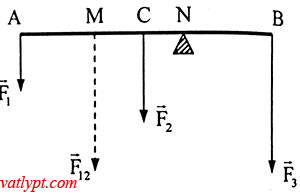
a/ F = F1 + F2 + F3 = 100N
xét với F12 = F1 + F2 = 50N đặt tại M như hình vẽ
F1/F2 = CM/AM = CM/(AC – CM) => CM = 20cm
xét với F = F12 + F3 sẽ đặt tại N như hình vẽ
BN/MN = F12/F3 = 1 => BN = MN = BM/2 = (AB – AM)/2 = 35cm
b/ Để thanh cân bằng phải đặt giá đỡ tại điểm N với BN = 35cm; AN = 65cm
Lực nén lên giá đỡ N = F = 100N
Bài tập 13. Thanh đồng chất ABC có tiết diện nhỏ, góc B = 60o treo cân bằng trên dây AD. Tính góc α tạo bởi BC và phương ngang biết BC = 2AB
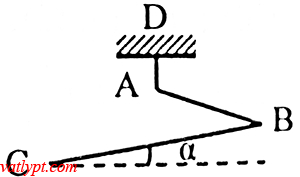
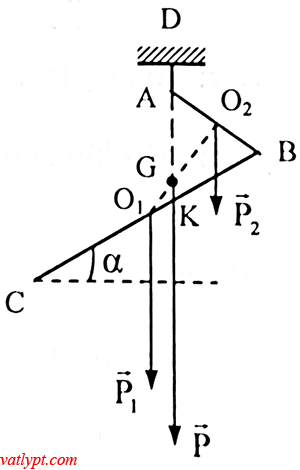
Các lực tác dụng lên thanh ABC: trọng lực P1 của BC, Trọng lực P2 của AB, lực căng T của dây AB
thanh treo cân bằng => →P1P1→ + →P2P2→ + ⃗TT→= ⃗00→
=> →P1P1→+→P2P2→ = ⃗PP→ = –⃗TT→
BC = 2AB => P1 = 2P2
P1.O1G = P2.O2G => P1/P2 = 2
=> P1/(P1 + P2) = O2G/(O1G + O2G) = O2G/O1O2 = 2/3
O1O2 = O1Bsin60o = O1B√3/2 => O2G = O1B√3/3
tanGAO2 = O2G/O2A = 2√3/3 => GAO2 = 49o => AKB = 180o – (60o + 49o) = 71o
=> α = 90o – 71o = 19o
Bài tập 14. Có 5 quả cầu nhỏ trọng lượng P; 2P; 3P; 4P; 5P gắn lần lượt trên thanh nhẹ, khoảng cách giữa hai quả cầu cạnh nhau là l. Tìm vị trí trọng tâm của hệ.
xG = (m1x1 + m2x2 + m3x3 + m4x4 + m5x5)/(m1 + m2 + m3 + m4 + m5)
=> xG = (2m2l + 3m3l + 4m4l + 5m5l)/(m + 2m + 3m + 4m + 5m) = 3,6l
Bài tập 15. Xác định vị trí khối tâm của các vật đồng chất sau.
a/ Đoạn dây nửa đường tròn bán kính R
b/ Bản bán nguyệt bán kính R
c/ Đoạn dây hình cung tròn bán kính R, góc α
d/ Bản hình quạt tròn bán kính R, góc α

Bài tập 16. Bản mỏng đồng chất cấu tạo từ hình bán nguyệt AOB bán kính R và hình chữ nhật cạnh AD = h. Xác định tỉ số h/R để trọng thâm của bản nằm tại O