Chương II: Bài tập lực hướng tâm
Chương II: Bài tập chuyển động của hệ vật
Bài tập lực hướng tâm, các dạng bài tập lực hướng tâm, phương pháp giải bài tập lực hướng tâm vật lý lớp 10 cơ bản nâng cao.
Bài tập lực hướng tâm
Bài tập 1. Bán kính Trái Đất là 6400km. Tính tốc độ dài, chu kỳ quay, độ lớn lực hấp dẫn tác dụng lên vệ tinh khối lượng 600kg chuyển động tròn đều quanh trái đất ở độ cao bằng bán kính trái đất, lấy g= 9,8 m/s2.
r=2*6400.103m; m=600kg, g=9,8m/s2
Lực hấp dẫn đóng vai trò lực hướng tâm => Fhd=Fht
Giải
Fhd=Fht => GMmr2GMmr2=mv2rv2r
g = GM/R2 => GM = gR2
=> v2=GMrGMr=gR2rgR2r => v=5600 m/s.
T=2π.rv2π.rv = 14354,3 s
Fhd=Fht=mv2rv2r = 1500 N.
Bài tập 2. Tính áp lực của ô tô 4 tấn đi qua điểm giữa cầu với tốc độ 72km/h, lấy g=10m/s2. Trong các trường hợp sau
a) cầu phẳng.
b) cầu cong lồi bán kính 100m
c) cầu cong lõm bán kính 200 m.

Chương II: Bài tập lực hướng tâm
v=72km/h=20m/s; r1=∞; r2=100m; r3=200m; g=10m/s2
Trọng lực P và phản lực N của mặt cầu đóng vai trò lực hướng tâm
→Fht=⃗P+⃗NFht→=P→+N→
xét về độ lớn phản lực N cân bằng với áp lực của ô tô nén lên mặt cầu nên về mặt tính toán ta coi N chính là độ lớn áp lực của ô tô lên mặt cầu.
Giải
a/ Cầu phẳng: Fht=0; N=P=mg=40000N
b/ Cầu cong lồi: Fht=P – N => N=P – Fht=mg – mv2rv2r=24000 N.
c/ Cầu cong lõm: -Fht=P – N => N=Fht + P=mg + mv2rv2r=56000 N.
Bài tập 3. Vật 400g buộc vào sợi dây không dãn người ta quay tròn vật trong mặt phẳng thẳng đứng. Dây dài 50cm, tốc độ góc 8 rad/s. Tính lực căng của sợi dây ở điểm cao nhất và điểm thấp nhất của quỹ đạo, lấy g=10m/s2

m=0,4kg; ω=8 rad/s; r=0,5m; g=10m/s2
Hợp của lực căng dây T và trọng lực P đóng vai trò lực hướng tâm
→Fht=⃗P+⃗TFht→=P→+T→
Chọn hệ qui chiếu gắn với mặt đất, chiều dương hướng xuống.
Giải
Ở điểm cao nhất: Fht= P + T=> T = mω2r – mg=8,8 N.
Ở điểm thấp nhất: – Fht = P – T=> T = mω2r + mg=16,8 N.
Bài tập 4. Vật khối lượng 500g treo vào sợi dây không giãn dài 50cm, chuyển động tròn đều trong mặt phẳng ngang biết sợi dây hợp với phương thẳng đứng góc 30o. Lấy g=10m/s2, tính tốc độ góc, tốc độ dài của vật và sức căng của sợi dây.
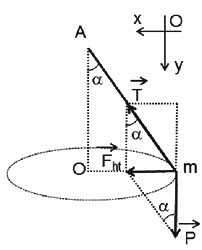
m=500g=0,5kg; α=30o, g=10m/s2; l=0,5m
Hợp của lực căng T, và trọng lực đóng vai trò lực hướng tâm
→Fht=⃗P+⃗TFht→=P→+T→
Chọn hệ trục tọa độ như hình vẽ
r=lsinα=0,25(m)
Giải
Fht=P.tanα=5√3/3 (N)
Fht=P.tanα => mv2lsinα=mgtanαmv2lsinα=mgtanα
=> v=√glsinαtanαglsinαtanα=1,2 m/s.
ω=v/r=4,8 rad/s
Fht=Tsinα => T=10√3/3 (N)
Bài tập 5. Vật khối lượng 500g treo vào sợi dây không giãn dài 2m, chuyển động tròn đều trong mặt phẳng ngang với tốc độ 30 vòng/phút. Lấy g=10m/s2, tính góc hợp bởi phương thẳng đứng và sợi dây, tính sức căng của sợi dây.
Bài tập 6. Một vật khối lượng 200 g đặt trên mặt bàn quay và cách trục quay 40 cm. Khi bàn quay với tốc độ 72 vòng/min thì vật vẫn nằm yên so với bàn. Tính độ lớn lực ma sát nghỉ của bàn tác dụng lên vật. (ĐS: 4,55 N).
m=0,2kg; r=0,4m; ω=72vòng/phút=2,4π (rad/s)
Giải
Fmsn=Fht=mω2r=4,55N
Bài tập 7: Mặt trăng quay 13 vòng quanh trái đất trong 1 năm. khoảng cách giũa trái đất và mặt trời gấp 390 lần khoảng cách giũa trái đất và mặt trăng. tính tỉ số khối lượng của mặt trời và trái đất?
Khoảng cách giữa mặt trăng và trái đất R => khoảng cách giữa mặt trời và trái đất r = 390R
Lực hấp dẫn giữa trái đất và mặt trời đóng vai trò lực hướng tâm
Gm1m2r2=m2ω21rGm1m2r2=m2ω12r
=> m1 = 4π2r3T21G4π2r3T12G (1)
Lực hấp dẫn giữa trái đất và mặt trăng đóng vai trò lực hướng tâm
Gm2m3R2=m3ω22RGm2m3R2=m3ω22R
=> m2 = 4π2R3T22G4π2R3T22G (2)
từ (1) và (2) => M1/M2 = 3,5.105
lưu ý trái đất quay 1 vòng quanh mặt trời mất 1 năm => T1 =1 năm
mặt trăng quay 13vòng quanh trái đất mất 1 năm => T2 = 1/13 năm
Bài tập 8. người đi xe đạp khối lượng tổng cộng 60kg trên vòng xiếc bán kính 6,4m phải đi qua điểm cao nhất với vận tốc tối thiểu bằng bao nhiêu để không rơi? Xác định lực nén lên vòng khi xe qua điểm cao nhất với vận tốc 10m/s.
Để xe đi qua được điểm cao nhất không rơi N = Q ≥ 0 => v ≥ √(gR) = 8m/s
v = 10m/s => Q = mv2/R – mg = 337,5N
Bài tập 9. Một máy bay thực hiện một vòng nhào lộn bán kính 400m trong mặt phẳng thẳng đứng với vận tốc 540km/h.
a/ Tìm lực do người lái có khối lượng 60kg nén lên ghế ngồi ở điểm cao nhất và thấp nhất của vòng nhào lộn.
b/ Muốn người lái không nén trên ghế ngồi ở điểm cao nhất của vòng nhào lộn thì vận tốc của máy bay phải là bao nhiêu.
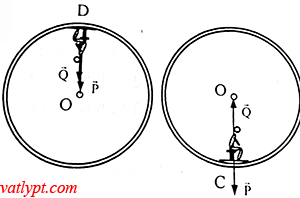
a/ Tại điểm cao nhất: P + Q = Fht => Q = mv2/R – mg = 2775N
Tại điểm thấp nhất: Q – P = Fht => Q = mv2/R + mg = 3975N
b/ Tại điểm cao nhất để Q = 0 = mv2/R – mg => v = √(gR) = 63,2m/s
Bài tập 10. Đoàn tàu chạy qua đường vòng bán kính 560m. Đường sắt rộng 1,4m và đường ray ngoài cao hơn đường ray trong 10cm. Tàu phải chạy với vận tốc bao nhiêu để gờ bánh không nén lên thành ray. Biết với α nhỏ tanα ≈ sinα
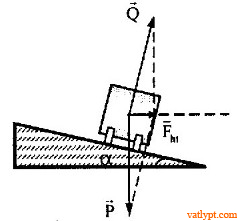
Qcosα = P => Q = P/cosα (1)
Để gờ bánh không nén lên đường ray thì
Qsinα = Fht = mv2/R (2)
từ (1) và (2) => mg.tanα = mv2/R => g.tanα = v2/R
tanα ≈ sinα = 10/140 => v = 20m/s = 72km/h
Bài tập 11. Quả cầu m = 50g treo ở đầu A của dây OA dài L = 90cm. Quay cho qủa cầu chuyển động tròn trong mặt phẳng thẳng đứng quanh tâm tâm O. Tìm lực căng của dây khi A ở vị trí thấp hơn O biết OA hợp với phương thẳng đứng góc 60o và vận tốc của quả cầu là 3m/s.
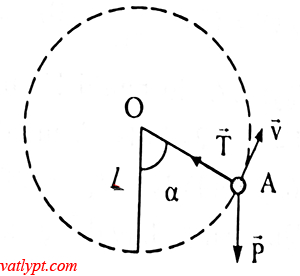
T – Pcosα = Fht = mv2/L => T = Pcosα + mv2/L
=> T = 0,75N
Bài tập 12. Vật khối lượng 0,1kg quay trong mặt phẳng thẳng đứng nhờ một dây treo có chiều dài l =1m, trục quay cách sàn H = 2m. Khi vật qua vị trí thấp nhất, dây treo đứt và rơi xuống sàn ở vị trí cách điểm đứt L = 4m theo phương ngang. Tìm lực căng của dây ngay khi dây sắp đứt.
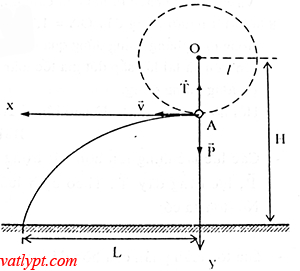
Thời gian vật chạm đất t = √2(H−l)g=1√52(H−l)g=15
Vận tốc của vật khi dây bị đứt: v = L/t = 4√5 (m/s)
Tại vị trí A trước khi dây sắp đứt
T – P = Fht = mv2/l => T = P + mv2/l = 9N
Bài tập 13. Hai quả cầu m1 = 2m2 nối với nhau bằng dây dài l = 12cm có thể chuyển động không ma sát trên một trục nằm ngang qua tâm của hai quả cầu. Cho hệ quay đều quanh trục thẳng đứng. Biết hai quả cầu đứng yên không trượt trên trục ngang. Tìm khoảng cách từ hai quả cầu đến trục quay.
Các quả cầu chuyển động tròn đều quanh trục bán kính khác nhau nhưng vận tốc góc là như nhau, lực căng dây đóng vai trò lực hướng tâm
=> m1ω2r1 = m2ω2r2 => m1r1 = m2r2 (1)
r1 + r2 = l (2)
từ (1) và (2) => r1 = 4cm; r2 = 8cm
Bài tâp 14. Một người dùng dây OA = 1,2m buộc vào một hòn đá tại A và quay tròn trong mặt phẳng thẳng đứng quanh tâm O. Khi dây bị đứt, hòn đá bay thẳng đứng lên trên, và tại lúc sắp đứt gia tốc toàn phần của hòn đá nghiêng góc α = 45o với phương thẳng đứng. Hòn đá lên được độ cao nhất bằng bao nhiêu kể từ vị trí dây bị đứt.
Gia tốc toàn phần ⃗aa→ = →anan→ + →atat→
→anan→: gia tốc pháp tuyến hướng vào tâm gây ra lực hướng tâm
→atat→: gia tốc tiếp tuyến
khi dây đứt T = 0; lúc dây sắp đứt α = 45o=> at = an => g = v2/l => v2 = gl
hmax = v2/2g = 0,6m
Bài tâp 15. Lò xo k = 50N/m, lo = 36cm treo vật m = 0,2kg có đầu trên cố định. Quay lò xo quanh một trục thẳng đứng qua đầu trên lò xo, m vạch một đường tròn nằm ngang hợp với trục lò xo góc 45o. Tính chiều dài của lò xo và số vòng quay trong 1 phút.
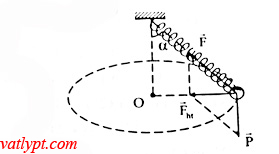
P = Fcos45o = > mg = k.Δlcos45 => Δl = 0,056m => l = Δl + lo = 0,416m
Fht = Ptan45o = mω2R = mg => ω = 5,8404 (rad/s) = 55,8 vòng/phút
Bài tâp 16. Hai lò xo giống hệt nhau k = 250N/m, lo = 36cm bố trí như hình vẽ. Hai vật m kích thước nhở có thể trượt không ma sát trên một trục ngang. Quay hệ quanh trục thẳng đứng với tần số n = 2 vòng/s. Cho m = 200g. Tính chiều dài mỗi lò xo
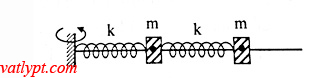
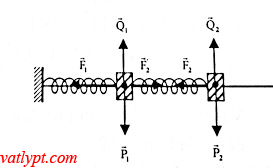
vật 1: →P1+→Q1+→F1+→F′1=m→a1P1→+Q1→+F1→+F1′→=ma1→
=> F1 – F’2 = ma = mω2(lo + Δl1) (1)
vật 2: →P2+→Q2+→F2=m→a1P2→+Q2→+F2→=ma1→
=> F2 = mω2(2lo + Δl1 + Δl2) (2)
ta có F2 = F’2 = kΔl2; F1 = k.Δl1 ; ω = 2π.n (rad/s);
thay vào (1) ; (2) giải hệ => Δl1 = 21cm; Δl2 = 14cm
=> l1 = 57cn; l2 = 50cm
Bài tâp 17. Đĩa nằm ngang quay quanh trục thẳng đứng với tần số n = 30vòng/phút. vật đặt trên mặt đĩa cách trục 20cm. hệ số ma sát giữa đĩa và vật là bao nhiêu để vật không trượt trên đĩa.
Lực ma sát nghỉ đóng vai trò lực hướng tâm
=> Fmsn = mω2r; để vật không trượt Fmsn < Fmst =. mω2r < µmg
=> µ > 0,2
Bài tâp 18. Đĩa tròn nhẵn có thể xoay quanh trục thẳng đứng vuông góc với mặt đĩa. Vật M đặt trên đĩa, cách trục quay R. vật m đặt trên M nối với trục bằng thanh nhẹ. Vận tốc quay của đĩa tăng chậm. hệ số ma sát giữa M và m là µ. Tính vận tốc góc ω của đĩa M để M bắt đầu trượt khỏi m.
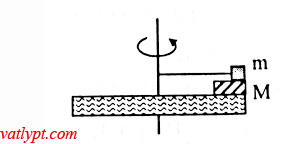
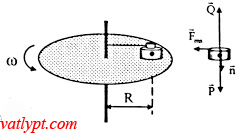
Khi vật M bắt đầu trượt khỏi m thì Fms = Fht
=> µmg = Mω2R => ω
Bài tâp 19. Một đĩa tròn nằm ngang có thể quay quanh một trục thẳng đứng. Vật m = 100g đặt trên đĩa, nối với trục quay bởi một lò xo nằm ngang. Nếu số vòng quay không quá ω1 = 2vòng/s, lò xo không biến dạng. Nếu số vòng quay tăng chậm đến ω2 = 5vòng/s lò xo dãn gấp đôi. Tính độ cứng k của lò xo.
ω1 = 2vòng/s = 4π (rad/s); ω2 = 5vòng/s = 10π (rad/s)
khi lò xo chưa biến đạng: Fms = Fht = m ω1lo
Khi lò xo biến dạng gấp đôi: Fht = Fđh + Fms
=> mω22lo = kΔl + m ω1lo = k(2lo – lo) + m ω1lo
=> k = m(2ω2 – ω1) = 182N/m
Bài tâp 20. Tìm vận tốc nhỏ nhất của một người đi moto chuyển động tròn đều theo một đường nằm ngang ở trong một hình trụ thẳng đứng bán kính 3m, hệ số ma sát trượt 0,3.
Fms = µQ = µFht = µmv2/R => v = 10m/s
Bài tập 21. Vận tốc tối đa của người đi xe đạp trên một đường vòng có mặt phẳng nghiêng về phía tâm một góc α gấp mấy lần vận tốc tối đa của xe đi trên đường vòng đó nhưng mặt đường nằm ngang. Coi bánh xe đều là bánh phát động.

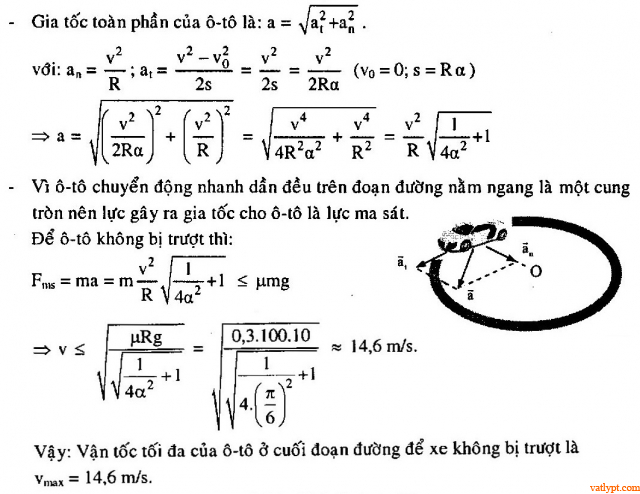
Bài tập 22. Ô tô chuyển động nhanh dần đều từ trạng thái nghỉ trên một đoạn đường nằm ngang là một cung tròn bán kính 100m, góc ở tâm α = 30o. Ô tô có thể đạt vận tốc tối đa nào ở cuối đoạn đường mà không bị trượt? Biết hệ số ma sát trượt µ = 0,3. Bỏ qua các ma sát cản chuyển động và coi các bánh xe đều là bánh phát động.
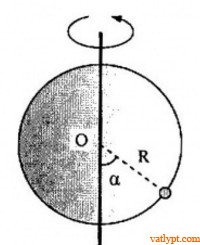
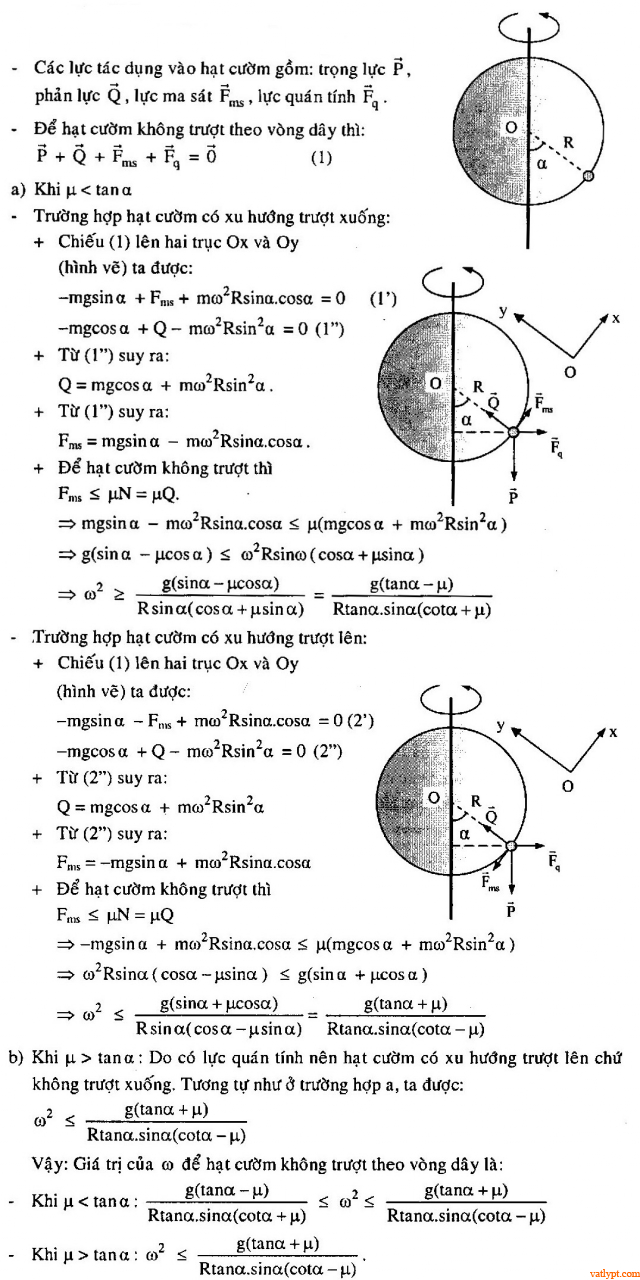
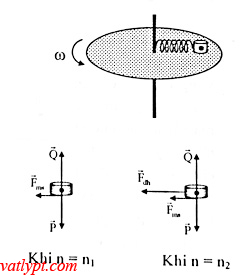
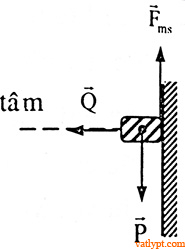
Bài tập 23. Một vòng dây cứng tâm O bán kính R được đặt thẳng đứng và quay nhanh một trục thẳng đứng qua tâm O. Một hạt cườm nhỏ khối lượng m bị xuyên qua bởi vòng dây và có thể trượt dọc theo vòng dây. Hệ số ma sát giữa hạt cườm và vòng dây là µ. Ban đầu hạt cườm ở vị trí α như hình vẽ. Xác định ω để hạt cườm không trượt theo vòng dây.