Phương pháp giải các bài toán đột biến thể lệch bội

Phương pháp giải các bài toán đột biến thể lệch bội

Bài tập tổng hợp cơ chế di truyền phân tử

Một số dạng toán thường gặp về đột biến thể lệch bội

I. Xác định số lượng  nhiễm sắc thể trong thể lệch bội 

Kiến thức cần nhớ :

Thể

Định nghĩa thể đột biến

 CT tính số lượng NST
Thể không Là hiện tượng tế bào bị mất 2 NST tương đồng trong cặp đó ( 2n – 2)
Thể một Là hiện tượng có 1 cặp NST chỉ mang 1 NST ( 2n -1 )
Thể ba Là hiện tượng có 1 cặp NST mang 3 NST  (2n + 1 )
Thể bốn Là trường hợp 1 cặp NST có  4 chiếc NST ( 2n + 2 )
Thể một kép Là trường hợp hai cặp NST tương đồng khác nhau , mỗi cặp đều chỉ biểu thị bằng 1  NST ( 2n – 1 – 1)

Cách giải :

  • Xác định số NST đơn bội của loài : n
  • Xác định dạng đột biến có trong tế bào , từ đó áp dụng các công thức tính số lượng NST trong tế bào
  • Chú ý dạng bài kiểu này có thể có sự kết hợp với tính số lượng NST trong chu kì tế bào nên cần ghi nhớ sự biến đổi số lượng NST trong tế bào.
Phương pháp giải các bài toán đột biến thể lệch bội

Phương pháp giải các bài toán đột biến thể lệch bội

Bài tập minh họa

Bài 1 : Một loài thực vật có bộ NST 2n = 24. Một tế bào sinh dục chín của thể ba nhiễm kép.  Tính  số NST các cặp NST đều phân li bình thường thì ở kì sau I số nhiễm sắc thể trong tế bào là

Hướng dẫn giải :

Ta có : n = 12 , thể ba nhiễm kép có 2 n + 1 +1 = 26 NST

Ở kì sau của giảm phân I NST tồn tại ở trạng thái kép và NST trong tế bào chưa phân li :

Số NST trong tế bào là 26 NST kép .

Bài 2 : Một tế bào sinh dưỡng của thể một kép đang ở kì sau nguyên phân, người ta đếm được 44 nhiễm sắc thể. Bộ nhiễm sắc thể lưỡng bội bình thường của loài này là bao nhiêu ?

Thể một kép 2n-1-1. kì sau nguyên phân, tế bào chưa phân chia, nhưng các NST kép đã tách ra thành 2 NST đơn. Người ta quan sát thấy 44 NST

Vậy số lượng NST trong tế bào khi chưa nhân đôi là   44 : 2 = 22

Thể một kép có số lượng NST trong tế bào là 2n -1 -1 = 22

Vậy số lượng NST trong bộ lưỡng bội của loài này là 22+1+1 = 24 (NST)

Bài 3 : Ở một loài thực vật lưỡng bội, trong tế bào sinh dưỡng có 6 nhóm gen liên kết. Thể một của loài này có số nhiễm sắc thể đơn trong mỗi tế bào khi đang ở kì sau của nguyên phân là

Tế bào sinh dưỡng có 6 nhóm gen liên kết tức là 2n =12

Thể một 2n – 1=11

Kì sau nguyên phân, tế bào chưa phân chia nhưng các NST kép đã chia làm đôi, di chuyển về 2 cực của tế bào. do đó số NST thể đơn là

11 x 2 = 22 (NST)

II.  Xác định số thể lệch bội của loài

– Thể khuyết: 2n – 2 ; Thể khuyết kép  : 2n – 2  – 2 .

– Thể 1: 2n – 1   ;  Thể 1 kép : 2n – 1 – 1 .

– Thể 3: 2n + 1   ;  Thể 3 kép : 2n + 1+ 1 .

– Thể 4: 2n + 2   ;  Thể 4 kép : 2n  + 2 + 2 .

Dạng đột biến Công thức tính số thể dột biến có thể xuất hiện 
Số dạng lệch bội đơn khác nhau     Cn1 = n
Số dạng lệch bội kép khác nhau    Cn2 = n(n – 1): 2
Có a  thể lệch bội khác nhau    Ana = n!:  (n –a)!= n ( n- 1 ) ..( n-a+1)

–          Xác định số NST đơn bội của loài : n

–          Xác định dạng đột biến có trong tế bào , từ đó áp dụng các công thức tính số thể đột biến .

Bài tập minh họa

Bài tập 1 : Bộ NST lưỡng bội của loài  = 24. Xác định:

– Có bao nhiêu trường hợp thể 3 có thể xảy ra?

– Có bao nhiêu trường hợp thể 1 kép có thể xảy ra?

– Có bao nhiêu trường hợp đồng thời xảy ra cả 3 đột biến; thể 0, thể 1 và thể 3?

Hướng dẫn giải :

Nhận xét

Thể 3 là trường hợp đột biến có liên quan đến 1 cặp NST => áp dụng công thức 1 .

Thể 1 kép là trường hợp đột biến có liên quan đến 2 NST => áp dụng công thức 2

Đông thời đột biến xảy ra ở thể 0, thể 1 và thể 3 => liên quan đến 3 NST => áp dụng công thức 3.

Sau khi phân tích xong ta tiến hành giải các yêu cầu của bài toán.

Số trường hợp thể 3 có thể xảy ra:  2n = 24→ n = 12

Số trường hợp thể 1 kép có thể xảy ra: Cn2 =  n(n – 1)/2 = 12.11/2 = 66

Số trường hợp đồng thời xảy ra cả 3 đột biến: thể 0, thể 1 và thể 3:

n(n – 1)(n – 2) = 12.11.10 =1320.

III. Xác định số loại giao tử của thể ba nhiễm

Cách tính nhanh giao tử thể ba nhiễm

Thể ba nhiễm sẽ tạo ra hai loại giao tử  \frac{1}{2} n và \frac{1}{2} n+1

Để xác định số loại giao tử của thể ba nhiễm => sử dụng sơ đồ hình tam giác

=>  Cạnh của tam giác chính là giao tử lưỡng bội cần tìm; đỉnh tam giác là giao tử đơn bội

=> Đối với kiểu gen AAa \rightarrow 1AA: 2 Aa : 2A : 1 a

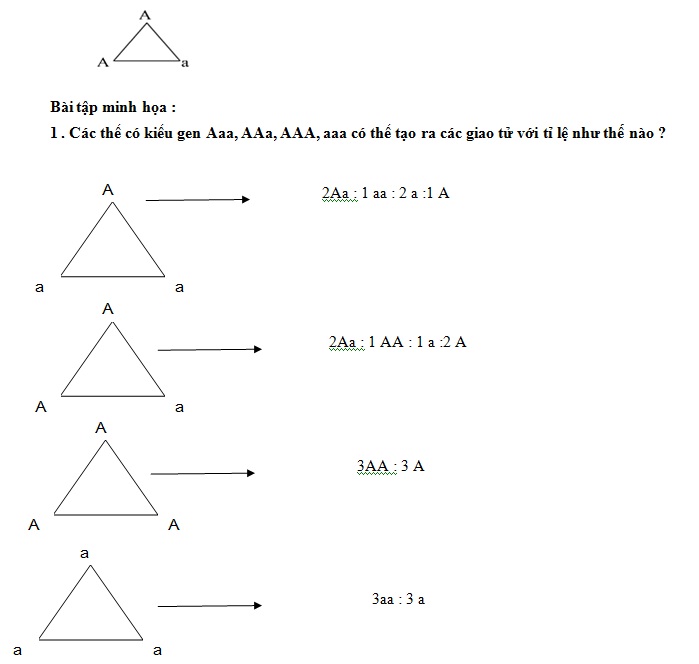
2 . Quy ước A – cao , a – thân thấp.  Xác định tỉ lệ kiểu gen và kiểu hình của  các phép lai sau :

P : Aaa x aaa

Hướng dẫn giải :

Ta có Aaa => 2Aa : 1aa : 1A : 2a;  aaa => 1aa : 1 a

Aaa x aaa = (2Aa : 1aa : 1A : 2a) x   ( 1aa : 1 a)  

                 = 2 Aaaa : 1aaaa : 1 Aaa : 2aaa : 2Aaa : 1aaa : 1Aa: 2 aa.

=> Tỷ lệ kiểu hình 6 cao : 16 thấp 

Thảo luận cho bài: Phương pháp giải các bài toán đột biến thể lệch bội