Chương II: Bài tập định luật Ôm, xác định giá trị cực đại
Chương II: Bài tập định luật Ôm phương pháp điểm nút
Bài tập định luật Ôm cho toàn mạch, phương pháp giải các bài tập tìm giá trị cực đại bài tập vật lý lớp 11 chương dòng điện không đổi
1/ Cơ sở lý thuyết
2/ Vận dụng các bài tập định luật Ôm cho đoạn mạch
Bài toán tổng quát: Cho đoạn mạch như hình vẽ:
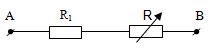
UAB = U = không đổi
R1 = b; R ≠ 0 là biến trở
a/ Xác định R để công suất trên điện trở R1 đạt giá trị cực đại, xác định giá trị cực đại
b/ Xác định R để công suất trên điện trở R đạt giá trị cực đại, xác định giá trị cực đại
c/ Xác định R để công suất toàn mạch đạt giá trị cực đại, xác định giá trị cực đại
Lưu ý: phương pháp trên áp dụng được cho cả mạch điện xoay chiều không phân nhánh RLC trong chương trình vật lý lớp 12.
3/ Bài tập định luật Ôm cho toàn mạch, phương pháp giải các bài tập tìm giá trị cực đại.
Bài tập 1: Cho mạch như hình vẽ:
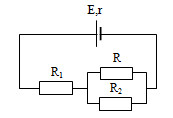
E=2V, r=0,7Ω , R1 = 0,3Ω , R2 = 2Ω
Xác định R để công suất của R đạt cực đại.
I = ER1+R2R+rER1+R2R+r = 21+R2R21+R2R
PR=U22RR=(IR2R)2RPR=U2R2R=(IR2R)2R
PR = 16R(3R+2)216R(3R+2)2 => (PR)max = 2/3W khi R = 2/3 (Ω)
Bài tập 2: Cho mạch điện như hình vẽ
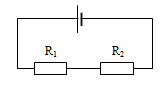
E=6V, r=1Ω, R2= 2Ω
a) Tìm R1 đểcông suất tỏa nhiệt trên R1max; Tính (P1 )max
b) Tìm R1 để công suất tỏa nhiệt toàn mạch max Tính Pmax
c) Tìm R1 để công suất tỏa nhiệt trên nguồn max tính (Png)max
P1=I2R1=(Er+R1+R2)2.R1P1=I2R1=(Er+R1+R2)2.R1
= 36R1(3+R1)236R1(3+R1)2=> (P1)max khi R1 = 3Ω => (P1)max = 3W
b/ P=I2(R1+R2+r)=363+R1P=I2(R1+R2+r)=363+R1=> Pmax khi R1 = 3Ω => Pmax = 6W
c/ Png=I2.r=36(3+R1)2Png=I2.r=36(3+R1)2
PngPngmax = 1W khi R1 = 3Ω
Bài tập 3: Cho mạch điện như hình vẽ
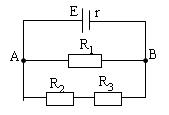
E=12V,r=2Ω,R1=4Ω,R2=2Ω. Tìm R3 để :
a) Công suất mạch ngoài lớn nhất, tính giá trị này
b) Công suất tiêu thụ trên R3 bằng 4,5W
c) Công suất tiêu tụ trên R3 là lớn nhất. Tính công suất này
PmaxPmax=E24E24 khi R = r = 2Ω => PmaxPmax=E24rE24r =18W
1RAB=1R1+1R231RAB=1R1+1R23 => R3 = 2Ω
b) R23 = R2 +R3 = R3 + 2
RAB =R1R23R1+R23R1R23R1+R23 =4(2+R3)6+R34(2+R3)6+R3
Cường độ mạch chính:
I=ERAB+rERAB+r=124(2+R3)6+R3+2124(2+R3)6+R3+2 =6(6+R3)10+3R36(6+R3)10+3R3
U23 =IRAB =24(2+R3)10+3R324(2+R3)10+3R3
I3 =U23R23U23R23=2410+3R32410+3R3
P3 =I32.R3 = 576R3(10+3R3)2576R3(10+3R3)2 = 4,5=> R3=509509
c) (P3)max = 576R3(10+3R3)2576R3(10+3R3)2 = 4,8W khi 3R3 = 10 => R3 = 10/3Ω
Bài tập 4: Cho mạch điện như hình vẽ
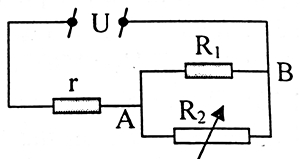
R1; r = 3Ω; R2 là biến trở. U =12V.
a/ Điều chỉnh R2 để công suất trên nó là lớn nhất, khi đó công suất trên R2 bằng 3 lần công suất trên R1. Tìm R1
b/ Thay R2 bằng một bóng đèn thì đèn sáng bình thường, khi đó công suất trên đoạn mạch AB là lớn nhất. Tính công suất và hiệu điện thế định mức của đèn.
U2 = UAB = I.RAB
P2 = U22/R2 = U2R12R2/(R2(r +R1) +rR1)2 = U2R21(√R2(r+R1)+rR1√R2)2U2R12(R2(r+R1)+rR1R2)2
P2 max khi mẫu min xảy ra khi √R2(r+R1)R2(r+R1) = \displaystyle \frac{rR_{1}}{\sqrt{R_{2}}\displaystyle \frac{rR_{1}}{\sqrt{R_{2}} => R2 = 3R1/(3+R1) (1)
=> P2max = U2.R1/[4r(r+R1)]
P2 = 3P1 = > R1 = 3R2 (2)
Từ (1) và (2) => R1 = 6Ω; R2 = 2Ω
b/ PAB = I2.RAB = U2.RAB /(r+RAB) => Pmax = U2/4r xảy ra khi RAB = r = 3Ω
RAB = R1.Rđ/(R1 + Rđ) => Rđ = 6Ω
Rđ = R1 => Pđ = P1 = PAB/2 = 6W => Uđ2 = Pđ.Rđ => Uđ = 6V
Bài tập 5: Cho mạch điện như hình vẽ.
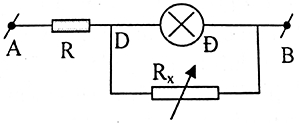
Biết R = 4Ω, đèn Đ:6V-3W, UAB = 9V không đổi. Rx là biến trở. Điện trở của đèn không đổi. Xác định giá trị của Rx để
a/ Đèn sáng bình thường
b/ Công suất tiêu thụ trên biến trở là lớn nhất. Tính công suất đó.
=> I = UAD/R = (UAB – Ux)/R = 0,75A
Ix = I – Iđm = 0,25A => Rx = Ux/Ix = 24Ω
b/ Ux = U – UAD = 27Rx/4(3+Rx)
Px = Ux2/Rx = 729Rx/[16(3 + Rx)2] => Px max = 3,8W khi Rx = 3Ω
