Chương I: Liên hệ dao động điều hòa với chuyển động tròn đều
Chương I: Dao động của con lắc lò xo
Nắm được lý thuyết liên hệ giữa dao động điều hòa và chuyển động tròn đều sẽ giúp bạn giải các bài toán liên quan đến thời gian, quãng đường trong dao động điều hòa được dễ dàng hơn.
Chương I: Liên hệ dao động điều hòa với chuyển động tròn đều
1/ Liên hệ giữa dao động điều hòa và chuyển động tròn đều:
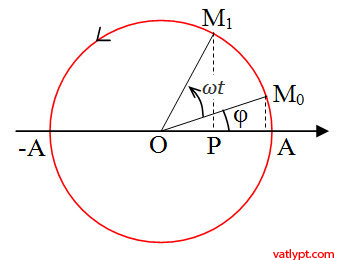
Xét một vật chuyển động tròn đều với tốc độ góc là ω trên quỹ đạo tròn bán kính A
Tại thời điểm ban đầu vật nằm tại vị trí điểm Mo hợp với phương ngang góc φ
Sau khoảng thời gian t vật chuyển động đến vị trí M1 góc mà nó quét được là ω.t
Hình chiếu của M1 lên phương ngang: OP=OM1.cos(ω.t + φ)
ta có: R=A=OMo=OM1 đặt OP=x =>
x=Acos(ω.t + φ)
đây chính là dạng phương trình của dao động điều hòa =>
 Dao động điều hòa là hình chiếu của chuyển động tròn đều
Dao động điều hòa là hình chiếu của chuyển động tròn đều2/ Vận dụng:
Trong khoảng thời gian một chu kỳ t=T chất điểm chuyển động tròn đều được một vòng (1 vòng=360o=2π)
x=Acos(ωt + φ) => các giá trị của x nằm trên trục cos (trục nằm ngang)
v=-ωAsin(ωt + φ) => các giá trị của v nằm trên trục sin (trục thẳng đứng)
Tại thời điểm ban đầu t=0 => x=Acosφ; v=-ωAsinφ
cho φ các giá trị đặc biệt trong lượng giác
φ =0; φ=30o=π/6; φ=45o=π/4; φ=60o=π/3; φ=90o=π/2 … ta sẽ tính được các giá trị của x; v và vẽ được đường tròn lượng giác như hình dưới.
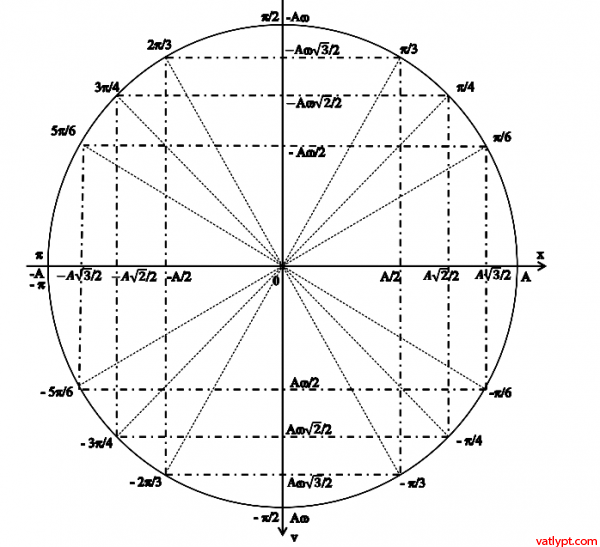
vòng tròn lượng giác giúp giải nhanh các bài tập trắc nghiệm dao động điều hòa
Ví dụ 1: Xác định khoảng thời gian ngắn nhất (theo chu kỳ T) vật dao động điều hòa chuyển động từ vị trí A/2 đến vị trí -A/2.
Hướng dẫn
Căn cứ vào đường tròn lượng giác ta có: Δφ=2π/3 – π/3=π/3
t=Δφω=TΔφ2π=T6t=Δφω=TΔφ2π=T6
Ví dụ 2: Một chất điểm dao động điều hòa với chu kì T. Gọi vTB là tốc độ trung bình của chất điểm trong một chu kì, v là tốc độ tức thời của chất điểm. Trong một chu kì, khoảng thời gian mà v ≥ (π/4)vTB là
A. T/2
B. T/3
C. 2T/3
D. T/6
Hướng dẫn
Vận tốc trung bình=quãng đường đi được / thời gian đi hết quãng đường đó
Trong 1 chu kỳ t=T; s=4A => vtb=4A/T=2Aω/π
=> (π/4).vtb = Aω/2 ứng với vị trí góc -π/6 (x=A√3/2) và -5π/6 (-A√3/2)
Trong quá trình dao động điều hòa, chuyển động của vật từ biên về vị trí cân bằng là chuyển động nhanh dần (vận tốc tăng dần) => v ≥ (π/4).vtb tương đương với khoảng thời gian vật chuyển động từ vị trí A√3/2 đến -A√3/2 (góc quét được Δφ=2π/3) và ngược lại từ vị trí -A√3/2 đến A√3/2 (góc quét được Δφ=2π/3)
=> t=2. (T.Δφ/2π)=2T/3
Ví dụ 3: Một chất điểm dao động điều hòa với chu kì T. Trong khoảng thời gian ngắn nhất khi đi từ vị trí biên có li độ x=A đến vị trí x=-A/2, chất điểm có tốc độ trung bình là
A. 6A/T
B. 9A/T
C. 3A/2T
D. 4A/T
Hướng dẫn
quãng đường vật đi được: s=A + A/2=3A/2
thời gian vật đi quãng đường trên: t = T.Δφ/2π=T. (2π/3)/2π=T/3
vận tốc trung bình vtb=s/t=9A/T
Ví dụ 4: Một chất điểm dao động điề hòa theo phương trình x=4cos(2π32π3t) (x tính bằng cm; t tính bằng s). Kể từ t=0, thời gian chất điểm đi qua vị trí có li độ x=-2 cm lần thứ 2011 là
A. 3015 s.
B. 6030 s.
C. 3016 s.
D. 6031 s.
Hướng dẫn
ω=2π/3 => T=2π/ω=3(s)
Tại thời điểm ban đầu t=0 => x=4.cos0=4cm=A
x=-2cm=-A/2
Trong 1 chu kỳ T chất điểm đi qua vị trí (-A/2) hai lần => thời gian chất điểm đi qua vị trí (-A/2) trong 2010 lần là
t1 = (2010/2).T=3015 (s)
Thời gian để chất điểm đi từ vị trí A đến vị trí -A/2 là
t2 = T.Δφ/2π=T/3=1(s)
=> thời gian chất điểm đi qua vị trí (-A/2) trong 2011 lần là
t=t1 + t2=3016(s)
