Chương III: Quy tắc hợp hai lực đồng quy
Chương III: Quy tắc hợp hai lực song song, cân bằng của vật rắn chịu tác dụng của ba lực song song
Quy tắc hợp hai lực đồng quy không song song cùng nằm trên mặt phẳng: trượt hai lực trên giá của chúng đến điểm đồng quy rồi áp dụng quy tắc hình bình hành để tìm hợp của hai lực đồng quy.
Chương III: Quy tắc hợp hai lực đồng quy
1/ Quy tắc hợp hai lực đồng quy đồng phẳng (cùng nằm trên mặt phẳng)
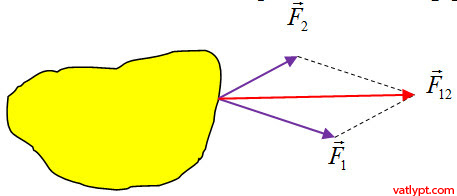
a/trường hợp 1: hợp hai lực đồng quy, đồng phẳng cùng tác dụng vào một vật rắn
Áp dụng quy tắc hình bình hành để tìm hợp của hai lực đồng quy tác dụng vào vật rắn
b/trường hợp 2: hai lực đồng phẳng, chưa đồng quy:
Trượt điểm đặt hai của hai lực trên giá của hai lực tác dụng vào vật rắn đến điểm đồng quy, sau đó áp dụng quy tắc hình bình hành để tìm hợp của hai lực đồng quy tác dụng vào vật rắn
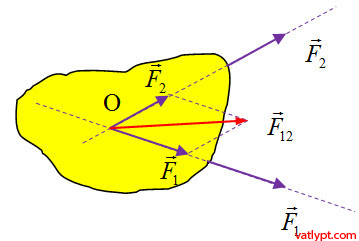
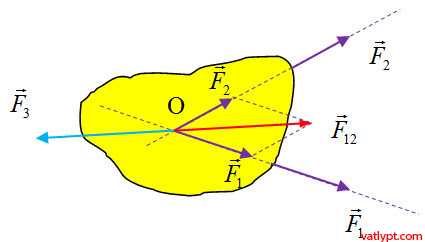
3/ Cân bằng của vật rắn chịu tác dụng của ba lực không song song
điều kiện cân bằng của vật rắn chịu tác dụng của hai lực không song song →F1+→F2=⃗0F1→+F2→=0→ tương đương với →F12+→F3=⃗0F12→+F3→=0→ = > →F3=−→F12F3→=−F12→
4/ Bài tập vận dụng quy tắc hợp hai lực đồng quy, cân bằng của vật rắn chịu tác dụng của ba lực không song song.
Bài toán 1: một diễn viên xiếc (coi là một vật rắn) trọng lượng 800N đi trên dây làm dây võng xuống một góc 1200. Tính lực căng của dây treo khi diễn viên xiếc đứng cân bằng (hình minh họa) coi dây không giãn.
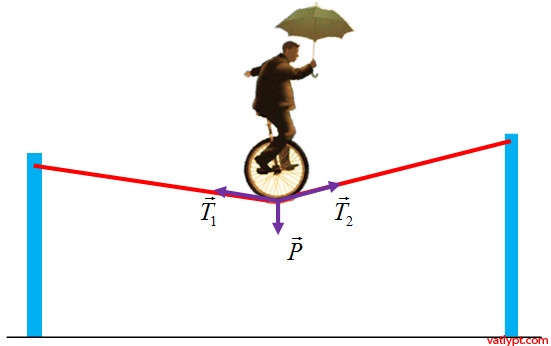
⃗P+→T1+→T2=⃗0P→+T1→+T2→=0→
Độ lớn: P=√T21+T22+2T1T2cos120P=T12+T22+2T1T2cos120
vì dây không giãn = > T1 = T2 = > T1 = T2 = P = 800N
