Chương I:Chuyển động tròn đều, gia tốc hướng tâm
Chương I: Chuyển động tròn biến đổi đều, gia tốc góc (Bài 10)
Chuyển động tròn đều là chuyển động cơ có quĩ đạo là đường tròn và có độ lớn vận tốc chuyển động không đổi theo thời gian.
Chương I:Chuyển động tròn đều, gia tốc hướng tâm
1/ Vận tốc của chuyển động tròn đều:
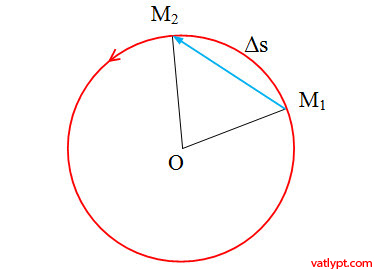
Tại thời điểm t1: chất điểm ở vị trí M1;
Tại thời điểm t2: chất điểm ở vị trí M2;
Trong khoảng thời gian Δt=t2 – t1
chất điểm chuyển động được quãng đường là Δs bằng độ dài của cung tròn M1M2
Vận tốc trung bình của chuyển động tròn đều
Xét trong khoảng thời gian Δt vô cung nhỏ điểm M1 rất gần với điểm M2 =>
Vận tốc tức thời của chuyển động tròn đều
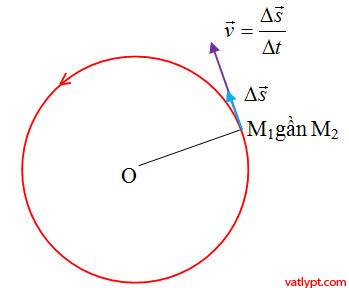
M1 rất gần M2 nên véc tơ độ dời Δ⃗sΔs→ có phương tiếp tuyến với quĩ đạo
=> véc tơ vận tốc sẽ có phương tiếp tuyến với đường tròn quĩ đạo tại điểm ta xét.
2/ Chu kỳ và tần số của chuyển động tròn đều
Chu kỳ lại đại lượng đặc trưng của chuyển động tròn đều được nhắc lại rất nhiều trong chương trình vật lý lớp 12 và ôn thi Đại học.
3/ Tốc độ góc của chuyển động tròn đều, liên hệ giữa tốc độ góc và tốc độ dài
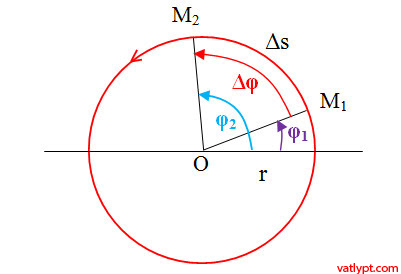
Tại thời điểm t1: chất điểm đang ở vị trí M1 hợp với phương ngang một góc φ1
Tại thời điểm t2: chất điểm ở vị trí M2 hợp với phương ngang một góc φ2
Trong khoảng thời gian Δt=t2 – t1 chất điểm chuyển động được một cung tròn Δs đồng thời bán kính quỹ đạo của nó cũng quét được một góc Δφ=φ2 – φ1
Công thức chuyển từ góc từ độ về radian (rad)
VD: 300=30π180=π630π180=π6; 900=90π180=π290π180=π2; 1200=120π180=2π3120π180=2π3
Khi vật chuyển động được 1 vòng tròn=3600=2π => 1 (vòng/s)=2π (rad/s)
Liên hệ giữa độ dài cung tròn và góc quét: Δs = r. Δφ =>
Tốc độ góc của chuyển động tròn đều còn được gọi là tần số góc.
4/ Gia tốc hướng tâm của chuyển động tròn đều
Gia tốc là đại lượng vật lý đặc trưng cho sự thay đổi của vận tốc cả về hướng và độ lớn. Trong chuyển động tròn đều độ lớn vận tốc của vật (tốc độ dài) không đổi nhưng hướng có thay đổi nên có tồn tại gia tốc.
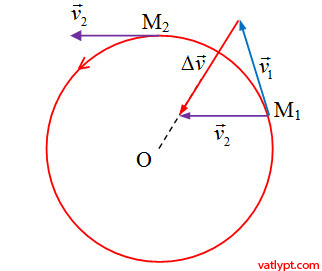
tại thời điểm t1 chất điểm ở vị trí M1, hướng của véc tơ vận tốc là →v1v1→
tại thời điểm t2 chất điểm ở vị trí M2, hướng của véc tơ vận tốc là →v2v2→
Tịnh tiến véc tơ →v2v2→ về vị trí M1 và thực hiện phép trừ véc tơ →v2−→v1v2→−v1→. Ta có v1=v2 (chuyển động tròn đều độ lớn của vận tốc là không đổi) => bằng toán học ta chứng minh được rằng véc tơ Δ⃗v=→v2−→v1Δv→=v2→−v1→ có chiều luôn hướng vào tâm O của chuyển động tròn đều.
Véc tơ gia tốc ⃗aa→ luôn cùng hướng với Δ⃗vΔv→ => gia tốc ⃗aa→ của chuyển động tròn đều luôn hướng vào tâm chuyển động nên được gọi là gia tốc hướng tâm viết tắt là aht hoặc →ahtaht→
